Asymmetric Relations

What Is an Asymmetric Relation?

A relation on a set X is said to be asymmetric if, whenever an element a is related to an element b, the reverse relation - b to a - does not hold. $$ a R b \ \ \Rightarrow b \require{cancel} \cancel{R} a $$

In an asymmetric relation, no two distinct elements are mutually related.

For instance, the relation “A is the mother of B” is asymmetric: if A is the mother of B, then B cannot be the mother of A.

Asymmetric relations belong to the broader class of relations defined on a set.

A Practical Example
Asymmetry vs. Antisymmetry
Further Remarks

A Practical Example

Consider the set:

$$ I = \{ 1, 2, 3, 4 \} $$

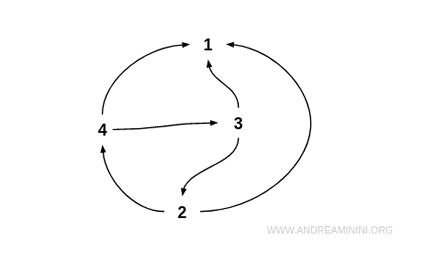
Let R be the relation “x is greater than y”:

$$ R = \{ (4;3), (4;2), (4;1), (3;2), (3;1), (2;1) \} $$

This relation is asymmetric because if x is greater than y, then y cannot be greater than x.

Note. For example, 4 is greater than 3: $$ 4 > 3 $$ but 3 is not greater than 4: $$ 3 < 4 $$ Thus, the relation satisfies the condition for asymmetry.

When represented as a graph, an asymmetric relation has no bidirectional edges between any pair of distinct nodes.

graph illustrating an asymmetric relation

Asymmetry vs. Antisymmetry

Asymmetry and antisymmetry are often confused, but they refer to different properties.

Antisymmetric relation
In an antisymmetric relation, two elements can be mutually related only if they are identical. In formal terms: if $ aRb $ and $ bRa $, then $ a = b $. Hence, if $ a \ne b $, it must follow that $ b \not\!Ra $. $$ aRb \ ,\ a \ne b \ \Rightarrow b \require{cancel} \cancel{R} a $$
Asymmetric relation
An asymmetric relation, on the other hand, forbids all reciprocal relations - no exceptions. Even if $ a = b $, the pair $ (a,a) $ cannot belong to the relation. $$ aRb \ \ \Rightarrow b \require{cancel} \cancel{R} a $$

In short, antisymmetry allows mutual relations only when the elements are equal, whereas asymmetry prohibits them entirely.

Further Remarks

Some key observations about asymmetric relations:

Not all relations are symmetric or asymmetric. If a relation is not asymmetric, that does not imply it is symmetric, and vice versa.
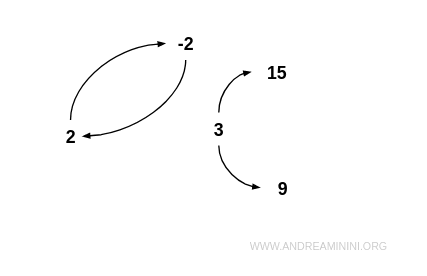
Example. Consider the set $$ I = \{ -2, 2, 3, 9, 15 \} $$ and the relation R defined as “x is a proper divisor of y”: $$ R = \{ (-2;2), (2;-2), (3;9), (3;15) \} $$ This relation is not asymmetric because - 2 and 2 are mutually related. However, it is not symmetric either, as the relation from 3 to 9 is not reciprocated. Therefore, R is neither symmetric nor asymmetric. In the graph, a two-way connection appears between - 2 and 2, but not among all node pairs.

And so on.