Order Relations

Order relations are mathematical relations that satisfy three key properties: reflexivity, antisymmetry, and transitivity.

• Reflexivity: $$ \forall \ a \in A \:\: a\rho a $$
• Antisymmetry: $$ \forall \ a,b \in A \ , \ a\rho b , \ a \ne b \Rightarrow b \require{cancel} \cancel{\rho} a $$
• Transitivity: $$ \forall \ a,b,c \in A :\: [ a\rho b \land b\rho c ] \rightarrow a\rho c $$

This type of relation is also known as a non-strict order relation.

There is also a related concept called a strict order relation, where the reflexive property is replaced with irreflexivity.

In general, a relation qualifies as an order relation if it is reflexive (or irreflexive), antisymmetric, and transitive.

A Practical Example

Let’s examine the set of natural numbers:

$$ N = \{ 1, 2, 3, 4, ... \} $$

We want to determine whether the relation R: "x is a multiple of y" is an order relation.

To decide, we verify whether it satisfies the three fundamental properties:

• Reflexive: Every number is a multiple of itself (e.g., x = 1·x).
• Antisymmetric: For distinct values x and y, if x is a multiple of y, then y is not a multiple of x.
• Transitive: If x is a multiple of y and y is a multiple of z, then x is a multiple of z.

Since all three conditions are met, R is an order relation.

Strict vs. Non-Strict Order Relations

Order relations fall into two broad categories:

• Non-strict order relations
  These satisfy reflexivity, antisymmetry, and transitivity.

  Example: The relation "x is a multiple of y" is a non-strict order. It’s reflexive (since every number is a multiple of itself, e.g., 2·1=2, 3·1=3, etc.), as well as antisymmetric and transitive.

• Strict order relations
  These satisfy irreflexivity, antisymmetry, and transitivity.

  Example: The relation "x is taller than y" is a strict order. It’s irreflexive (no one can be taller than themselves), and also satisfies antisymmetry and transitivity.

In short, strict orders are irreflexive, while non-strict orders are reflexive.

Total vs. Partial Order Relations

Both strict and non-strict order relations can further be classified based on how completely they organize a set. An order relation is either total or partial:

• Partial order relation

  A partial order relates only some elements within a set, meaning not all pairs of elements can be compared.

  It applies to only a subset of the Cartesian product. In such cases, the set is known as a partially ordered set. Only certain pairs of elements are comparable.

  Example: The power set P(X) of X = {1, 2, 3} consists of the elements: {∅, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}. Under the inclusion relation ⊆, this forms a partially ordered set: for instance, {1} ⊆ {1,2}, but {3} is not a subset of {1,2}. The structure is visualized as follows:
  

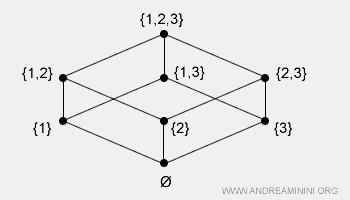
• Total order relation

  A total order relates all elements of the set - any two elements can be compared.

  This applies to every pair (a, b) in the set. In this case, the set is known as a totally ordered set, or a chain, because of its vertical structure: every pair is comparable.

  Example: The same set X = {1, 2, 3} can be totally ordered using the relation ≤ (or ≥). In this setting, every pair of elements is comparable: 1ρ2, 2ρ3, 1ρ3, and so on. The corresponding diagram forms a chain, as each element is directly comparable to the others.
  

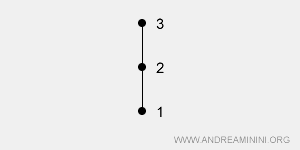
Visualizing Order Relations

Order relations on a set X can be represented using diagrams with points and connecting lines.

Each point corresponds to an element of the set.

A line segment connects two elements that are directly comparable under the relation - meaning no intermediate element lies between them.

Example: In the relation ≤, elements 1 and 3 are comparable. However, since 2 lies between them, no direct link is drawn. In contrast, 1 and 2 are connected, as there’s no element in between. The same applies to 2 and 3.

Isomorphic Ordered Sets

Two ordered sets are said to be isomorphic if they share the same structural pattern of relationships.

For instance, any totally ordered sets with the same number of elements (cardinality) are always isomorphic.

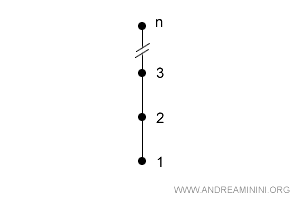
In short, isomorphic sets have the same relational structure between their elements, even if the elements themselves differ.

And so on.