Characterizing Disconnected Sets Using Open Sets in a Topological Space

This means that whenever a set \(A\) is disconnected, we can always find two disjoint, nonempty open sets in \(X\) that capture the two separate pieces of \(A\).

Conversely, the existence of such open sets guarantees that \(A\) is disconnected.

Why does this matter?

This characterization gives a concrete way to determine whether a subset \(A\) is disconnected within the ambient topological space \(X\), relying entirely on the structure of the open sets of \(X\).

A concrete example

Consider the subset \(A\) of the real line \(\mathbb{R}\):

$$ A = [0,1] \cup [2,3] \in X = \mathbb{R}  $$

It is immediately clear that \(A\) is disconnected since it consists of two disjoint intervals:

• \([0,1]\)
• \([2,3]\)

The theorem tells us that there must be two open sets in \(X\) that separate these two pieces.

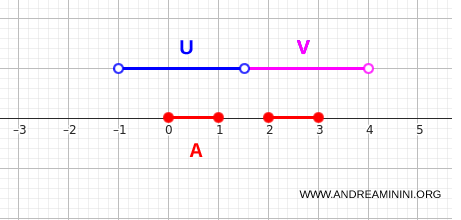
Choose two open intervals in \(\mathbb{R}\) that each intersect one of the components of \(A\):

• $ U = (-1,1.5) $
• $ V = (1.5,4) $

Both intervals are open subsets of the real line.

Their intersections with \(A\) are nonempty:

$$ U \cap A = [0,1] \neq \varnothing $$

$$ V \cap A = [2,3] \neq \varnothing $$

And they do not overlap on any part of \(A\):

$$ (U \cap V) \cap A = \varnothing $$

This shows that the two open intervals separate \(A\) into two disconnected components.

Hence \(A\) is disconnected in \(\mathbb{R}\).

Example 2

Now consider a set consisting of just two points in \(\mathbb{R}\):

$$ A = \{1, 3\} \in X = \mathbb{R} $$

This set is disconnected because the points are isolated from each other, with no continuous path lying entirely inside \(A\) joining them.

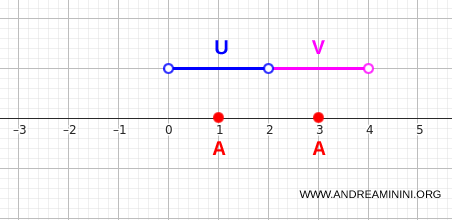
To verify this via the open-set characterization, take:

$$ U = (0,2) $$

$$ V = (2,4) $$

Each one contains exactly one element of \(A\):

$$ U \cap A = \{1\} $$

$$ V \cap A = \{3\} $$

And their overlap contains no point of \(A\):

$$ U \cap V \cap A = \varnothing $$

Thus \(A\) decomposes into two nonempty and disjoint sets that are open in the subspace topology. 

Therefore \(A\) is disconnected in \(\mathbb{R}\).

Example 3

Consider the plane \(\mathbb{R}^2\) with the entire \(x\)-axis removed:

$$ A = \{(x,y) \in \mathbb{R}^2 : y>0\} \cup \{(x,y) \in \mathbb{R}^2 : y<0\} $$

This set is disconnected: the open upper and lower half-planes are separated by a missing line.

Select the open sets:

$$ U = \{(x,y) : y> -1\} $$

$$ V = \{(x,y) : y< 1\} $$

These intersect \(A\) as follows:

• \(U \cap A\) contains the entire open upper half-plane
• \(V \cap A\) contains the entire open lower half-plane

No point of \(A\) lies in their intersection:

$$ (U \cap V) \cap A = \varnothing $$

Hence \(A\) is disconnected.

Proof

The proof breaks naturally into two directions.

A] If such open sets exist, then \(A\) is disconnected

Assume there exist open sets \(U\) and \(V\) in \(X\) satisfying the four conditions.

Define:

\[ P = U \cap A, \qquad Q = V \cap A \]

Under our assumptions:

• \(P\) and \(Q\) are nonempty
• \(P\) and \(Q\) are open in the subspace topology
• \(P \cap Q = (U \cap V) \cap A = \varnothing\)
• \(P \cup Q = A\) because \(A \subset U \cup V\)

Thus \((P,Q)\) is a separation of \(A\).

Therefore \(A\) is disconnected.

B] If \(A\) is disconnected, then such open sets exist

Now assume that \(A\) is disconnected.

By definition, \(A\) admits a separation, that is, two nonempty subsets

$$ P, Q \subset A $$

such that:

• each is open in the subspace topology on \(A\)
• they are disjoint
• they satisfy \(P \cup Q = A\)

Since \(P\) is open in \(A\), there exists an open set \(U\) in \(X\) with

$$ P = U \cap A $$

Likewise, because \(Q\) is open in \(A\), there exists an open set \(V\) in \(X\) with

$$ Q = V \cap A $$

We check the required conditions:

• From \(A = (U \cap A) \cup (V \cap A)\) we obtain \(A \subset U \cup V\)
• \(U \cap A = P \neq \varnothing\)
• \(V \cap A = Q \neq \varnothing\)
• \((U \cap V) \cap A = (U \cap A) \cap (V \cap A) = P \cap Q = \varnothing\)

All conditions are met.

Thus suitable open sets in \(X\) exist that separate \(A\).

C] Conclusion

We have shown that a subset \(A\) of a topological space \(X\) is disconnected if and only if it can be covered by two open sets that partition it into two nonempty, disjoint subsets.

This completes the argument.