Theorem: Characterization of Connected Spaces via Open and Closed (Clopen) Sets

A topological space \( X \) is connected if and only if the only subsets of \( X \) that are both open and closed (that is, clopen) are \( X \) itself and the empty set \( \emptyset \).

Equivalently, a topological space is connected when the only clopen sets are the trivial ones: the entire space and the empty set.

In other words, there are no non-empty proper subsets of \( X \) that are simultaneously open and closed.

This theorem provides a fundamental criterion for determining whether a topological space is connected.

Explanation

In topology, a subset that is both open and closed effectively separates the space into two disjoint non-empty open subsets.

If such a non-trivial clopen set exists, meaning one that is neither \( X \) nor \( \emptyset \), the space can be decomposed into two disjoint open subsets, each non-empty, with no continuous connection between them.

This implies that the space is disconnected.

Conversely, if the only clopen subsets of \( X \) are \( X \) and \( \emptyset \), then no separation of \( X \) into disjoint non-empty open subsets is possible, and therefore the space is connected.

Note. In any topological space, both the entire set \( X \) and the empty set \( \emptyset \) are always open and closed.

Example 1

Consider the set \( X = \{ a, b, c, d \} \) equipped with the topology \( T \), where the open sets are defined as follows: \( \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \}, \emptyset \).

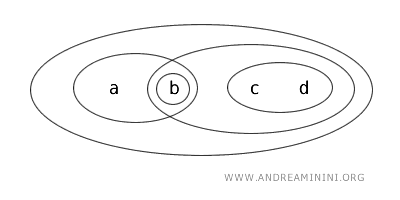
In this case, the subset \( \{ a, b \} \) is clopen, that is, both open and closed.

• It is open because it is explicitly listed as an open set in the topology \( T \).
• It is closed because its complement \( X \setminus \{ a, b \} = \{ c, d \} \) is also open in \( T \).

Hence, the topological space \( (X, T) \) is disconnected, since there exists a proper non-empty subset that is clopen.

The existence of even one non-trivial clopen subset is sufficient to conclude that a space is disconnected.

The mere presence of a clopen subset distinct from \( X \) and \( \emptyset \) shows that the space can be expressed as the union of two disjoint non-empty open subsets, \( \{ a, b \} \) and \( \{ c, d \} \). Thus, the condition for topological connectedness is not satisfied.

Example 2

Consider the set of real numbers \( \mathbb{R} \) endowed with the standard topology, that is, the topology generated by open intervals \( (a, b) \).

In this topology, the intervals \( (a, b) \) are open but not closed, while the intervals \( [a, b] \) are closed but not open.

The only subsets of \( \mathbb{R} \) that are both open and closed are \( \mathbb{R} \) itself and \( \emptyset \).

Therefore, the space \( \mathbb{R} \) with the standard topology is connected.

Example 3

Now consider the subspace \( X = (0,1) \cup (2,3) \subset \mathbb{R} \) with the topology induced by the standard topology on \( \mathbb{R} \).

In this case, the subsets \( (0,1) \) and \( (2,3) \) are both open in \( X \) and closed in \( X \), since the complement of each within \( X \) is the other open interval. Specifically:

• The complement of \( (0,1) \) in \( X \) is \( (2,3) \), which is open in \( X \).
• The complement of \( (2,3) \) in \( X \) is \( (0,1) \), which is also open in \( X \).

Thus, both subsets are clopen.

Since there exist non-trivial subsets that are simultaneously open and closed, the subspace \( X \) is disconnected.

This disconnection arises because \( X \) can be represented as the union of two disjoint non-empty open subsets, \( (0,1) \) and \( (2,3) \), which together cover the entire space.