Connectedness via a Common Intersection

Let \( C_1, C_2, \dots, C_n \subset X \) be a collection of connected subsets of a topological space \( X \) such that they share at least one common point: \[
\bigcap_{i=1}^n C_i \neq \varnothing . \] Then their union \( \bigcup_{i=1}^n C_i  \) is a connected set.

In other words, whenever two or more connected subsets of \( X \) have at least one point in common, their union remains connected.

This result makes explicit use of the assumption that the intersection of all the sets is non-empty.

Note. The condition \( \bigcap_{i=1}^n C_i \neq \varnothing \) is sufficient to guarantee that the union \( \bigcup_{i=1}^n C_i \) is connected, but it is not a necessary condition. Indeed, a union of connected sets may still be connected even when there is no single point common to all of them. This occurs, for example, in situations involving chain intersections.

A concrete example

Consider the following subsets of \( \mathbb{R}^2 \):

• \( C_1 \): the horizontal segment from \( (-1,0) \) to \( (1,0) \)
• \( C_2 \): the vertical segment from \( (0,-1) \) to \( (0,1) \)
• \( C_3 \): the diagonal segment joining \( (-1,-1) \) to \( (1,1) \)

Each of these sets is connected.

Moreover, they all contain the point \( (0,0) \). Indeed:

\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]

Hence, the common intersection is non-empty:

\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]

As a result, by the connectedness criterion, their union is a connected set:

\[ C_1 \cup C_2 \cup C_3  \]

All three segments meet at the same central point. This ensures that the union is connected.

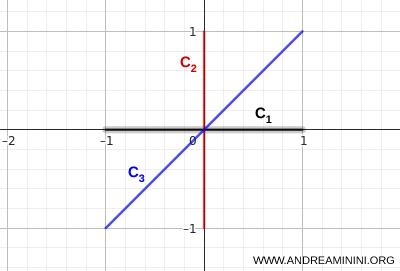
From any point on one segment, it is possible to reach any other point by moving exclusively through points belonging to the union.

Note. There exist other connectedness criteria that do not require all sets \( C_i \) to share a common point, that is, they do not require \( \bigcap_i C_i \neq \varnothing \). For example, if the sets \( C_i \) are connected and intersect in a chain, meaning that \( C_i \cap C_{i+1} \neq \varnothing \), then their union \( \bigcup_i C_i \) is connected even if \( \bigcap_i C_i = \varnothing \). However, the chain-intersection condition is not necessary either, since the union may still be connected even when some consecutive pairs are disjoint, provided that other sets in the family act as bridges. For instance, consider three segments forming a triangle. Their total intersection is empty, \( \bigcap_i C_i = \varnothing \), yet the union is connected.

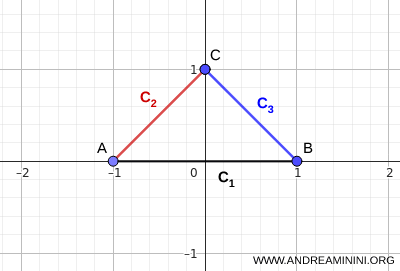
This example clearly illustrates that chain intersection is sufficient to guarantee the connectedness of the union.

Proof

Let \( X \) be a topological space and let \( \{C_i\}_{i \in I} \) be a family of connected subsets of \( X \) with a non-empty common intersection:

\[ \bigcap_{i \in I} C_i \neq \varnothing \]

Suppose, for the sake of contradiction, that the union

\[ C = \bigcup_{i \in I} C_i \]

is not connected.

If \( C \) is not connected, then there exist two open sets \( U \) and \( V \) that form a separation of \( C \), meaning that:

• \( U \cap C \neq \varnothing \)
• \( V \cap C \neq \varnothing \)
• \( (U \cap C) \cap (V \cap C) = \varnothing \)
• \( C = (U \cap C) \cup (V \cap C) \)

Since, by assumption, the intersection of the sets \( C_i \) is non-empty,

\[ \bigcap_{i \in I} C_i \neq \varnothing \]

there exists a point \( x \in C \) that belongs to every set \( C_i \):

\[ x \in \bigcap_{i \in I} C_i \]

This common point must lie in either \( U \) or \( V \), but not in both, since they form a separation of \( C \). Suppose, without loss of generality, that

\[ x \in U \quad \text{and} \quad x \notin V \]

Since each set \( C_i \subset C \), we may write:

\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]

Because \( C_i \cap U \) and \( C_i \cap V \) are open in the subspace topology on \( C_i \), disjoint, and together cover \( C_i \), and since each \( C_i \) is connected by hypothesis, one of the two sets must be empty.

Therefore, each \( C_i \) must be entirely contained in either \( U \) or \( V \):

\[ C_i \subset U \quad \text{or} \quad C_i \subset V \]

If \( x \in C_i \) and \( x \in U \), then it cannot be the case that \( C_i \subset V \).

It follows that:

\[ C_i \subset U \quad \text{for every } i \in I \]

Hence, the union \( C \) is a subset of \( U \):

\[ \bigcup_{i \in I} C_i \subset U \]

This contradicts the assumption that \( V \cap C \neq \varnothing \).

The contradiction shows that the initial assumption is false. Therefore, the union \( \bigcup_{i \in I} C_i \) is a connected set.

And so on.