Connected Space

Definition using open sets

In simpler terms, a space is topologically connected when it cannot be split into two nonempty, disjoint open subsets whose union makes up the entire space.

If such a pair of open sets exists, the space is disconnected, and the pair ( (U, V) ) is called a separation of ( X ).

Note. This is the definition of topological connectedness in terms of open sets. As we will see, this notion differs from "path connectedness" or "arc connectedness." The two are not always equivalent.

A practical example

Consider the set $ X $ consisting of three elements:

$$ X = {a, b, c} $$

We define two different topologies on $ X $:

• Topology A
  The open sets are $$ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $$
• Topology B
  The open sets are $$ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $$

Which of the two spaces is connected?

By definition, a topological space ( X ) is connected if there are no two nonempty, disjoint open sets whose union equals ( X ).

If such a pair exists, it forms a separation of ( X ), and the space is disconnected.

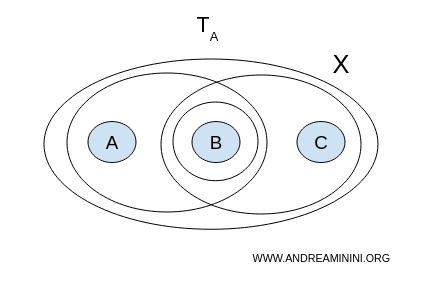
1] Topology A

Let us search for a separation $ (U, V) $ within the topology $ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $, that is, two nonempty, disjoint open sets whose union covers the entire space $ X $.

• $ U = {a,b}, V = {b,c} $ are not disjoint, since they both contain $ b $;
• $ U = {a,b}, V = {b} $ are not disjoint;
• $ U = {b}, V = {b,c} $ are not disjoint.

No pair of nonempty, disjoint open sets covers $ X $ completely.

Therefore, with topology $ A $, the topological space $ X $ is connected.

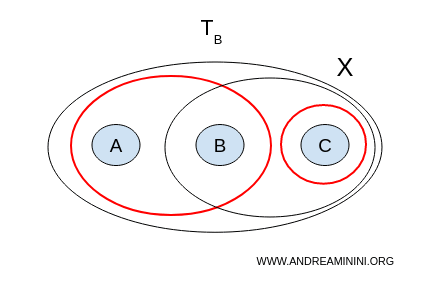
2] Topology B

Now, let us look for a separation $ (U, V) $ in the topology $ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $.

• $ U = {a,b}, V = {b,c} $ are not disjoint, since they both contain $ b $;
• $ U = {a,b}, V = {c} $ are nonempty, disjoint, and their union covers the entire space: $ U \cup V = {a,b,c} = X $.

This last pair ( $ U = {a,b}, V = {c} $ ) satisfies all the conditions for a separation, so the space $ X $ with topology B is disconnected.

Note. This example shows that connectedness depends not only on the underlying set but also on the chosen topology. Even with the same set of points, the two topologies yield different global properties: the first preserves connectedness, while the second breaks it.

Example 2

Consider the space $ X $ where $ n $ is a fixed real number (for instance $ n = 0 $):

$$ X = (-\infty, n) \cup (n, +\infty) $$

This set represents the real line with one point removed:

$$ X = \mathbb{R} \setminus {n} $$

Is this space connected or disconnected?

The sets $ U = (-\infty, n) \quad \text{and} \quad V = (n, +\infty) $ are both:

• open in the standard topology on $ \mathbb{R} $;
• disjoint, since they share no points;
• nonempty.

Their union $ U \cup V $ is exactly $ X $:

$$ U \neq \emptyset, \quad V \neq \emptyset, \quad U \cap V = \emptyset, \quad U \cup V = X $$

This fits precisely the definition of a separation of the space.

Hence, the space $ X = (-\infty, n) \cup (n, +\infty) $ is disconnected, because it can be divided into two nonempty, disjoint open subsets whose union covers the whole space.

Note. In general, removing a single point $ n $ from the real line "breaks" its continuity. The line splits into two separate parts - one to the left and one to the right of $ n $ - that can no longer be joined by any continuous path. For this reason, the space is not only disconnected in the topological sense but also not path-connected.

The distinction between connected and path-connected spaces

Topological connectedness and path connectedness are not always the same.

A topological space may be connected without being path-connected (or arc-connected).

• Topological connectedness
  The space cannot be divided into two disjoint, nonempty open subsets whose union is the entire space.
• Path connectedness
  For every pair of points in the space, there exists a continuous path lying entirely within the space that joins them. If the path never passes through the same point twice, the space is said to be arc-connected.

In general, every path-connected space is connected, but not every connected space is path-connected.

A continuous path between two points prevents the space from being "cut" into two separate open regions.

However, the converse does not hold: there exist connected spaces that are not path-connected.

Example. A classic example is the topologist's sine curve: $$ S = { (x, \sin(1/x)) \mid x > 0 } \cup { (0, y) \mid -1 \le y \le 1 } $$ This space is connected, since it cannot be split into two disjoint open sets, but it is not path-connected, because no continuous path can join a point on the oscillating curve to a point on the vertical segment.

Notes

Additional observations on connected spaces

• Theorem: Characterization of Connected Spaces through Open and Closed (Clopen) Sets
  A topological space \( X \) is connected if and only if the only subsets of \( X \) that are both open and closed (clopen) are \( X \) itself and the empty set \( \emptyset \).

And so on.