Separation of a Subset by Open Sets

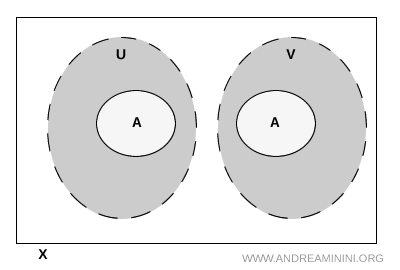
Let $ A $ be a subset of a topological space $ X $. The open sets $ U $ and $ V $ in $ X $ are said to form a separation of $ A $ when the following conditions hold:

They cover $ A $ \[ A \subseteq U \cup V \]
Each intersects $ A $ non trivially \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
They are disjoint on $ A $ \[ U \cap V \cap A = \varnothing \]

In essence, the set $ A $ is split into two disjoint pieces, one lying in $ U $ and the other in $ V $, with no overlap between them inside $ A $.

This notion provides the standard topological way to express that a subset is separated.

diagram illustrating the separation of a subset by open sets

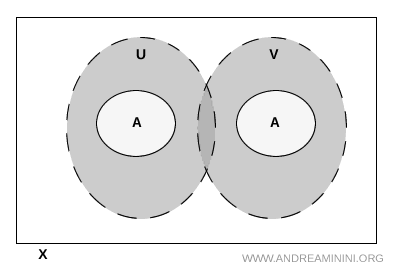
Nota. The sets $ U $ and $ V $ need not be disjoint in the entire ambient space $ X $. They may intersect outside $ A $. What matters is that their intersection does not meet $ A $.
diagram showing that U and V may intersect outside the subset A

A Practical Example

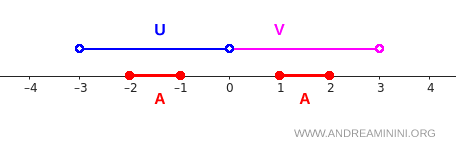
Consider the topological space $ X = \mathbb{R} $ with the standard topology, and let $ A $ consist of two disjoint closed intervals:

$$ A = [-2,-1] \cup [1,2] $$

Define the following open subsets of $ X $:

$$ U = (-3,0) $$

$$ V = (0,3) $$

The intervals can be visualized as follows:

graph of the open sets U and V together with the subset A

We now verify the separation conditions.

The interval $ [-2,-1] $, which forms part of $ A $, lies entirely in $ U $.

The interval $ [1,2] $, the other component of $ A $, lies entirely in $ V $.

Hence:

$$ A \subseteq U \cup V $$

Each open set meets $ A $ in a non empty set:

$$ U \cap A = [-2,-1] \neq \varnothing $$

$$ V \cap A = [1,2] \neq \varnothing $$

And $ U $ and $ V $ do not intersect within $ A $:

$$ U \cap V \cap A = \varnothing $$

Thus the open sets $ U $ and $ V $ indeed form a separation of the subset $ A $ in the space $ X $.