Every connected subset is contained in a single connected component

Let $ A $ and $ B $ be subsets of a topological space $ X $, with $ A $ connected and $ A \subset B $. If $ B $ admits a separation into two subsets $ B_1 $ and $ B_2 $ in $ X $, then $ A $ must be entirely contained in exactly one of these two subsets: $$ A \subset B_1 \quad \text{or} \quad A \subset B_2 $$

A connected set cannot intersect both sides of a separation.

If it lies within a set that splits into two disjoint subsets, then it must lie wholly within one of them.

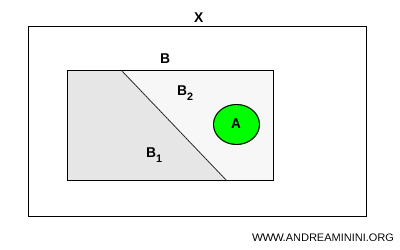
connected subset lying entirely within one part of a separation

Intuitively, a connected set behaves like a single, unbroken piece of rope placed inside an envelope. If the envelope is divided into two disjoint compartments while the rope remains intact, then the rope must lie entirely within one compartment. Otherwise, it would have to be torn. Connectedness prevents a set from straddling a separation, just as an intact rope cannot be divided without breaking.

A concrete example
Proof

A concrete example

Consider the topological space:

$$ X = \mathbb{R} $$

and the following subset of $ X $:

$$ B = (-3,4) $$

This set can be separated into the two subsets:

$$ B_1 = (-3,0) $$

$$ B_2 = (0,4) $$

These two subsets are disjoint:

$$ B_1 \cap B_2 = \varnothing $$

and their union is exactly $ B $:

$$ B_1 \cup B_2 = B $$

Moreover, $ B_1 $ and $ B_2 $ are open in the subspace topology on $ B $.

They therefore form a separation of $ B $ in $ X $.

Now consider a connected subset of $ B $:

$$ A = (1,2) $$

Since $ A \subset B_2 $, the set $ A $ lies entirely within one of the two subsets of the separation.

Note. If instead we take $ A = (-1,1) $, then we find that $$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ This situation cannot occur, because $ B_1 $ and $ B_2 $ form a separation of $ B $. A connected subset of $ B $ cannot be distributed across both subsets of a separation. If this were possible, then $ A $ itself would admit a separation, contradicting the fact that the interval $ (-1,1) $ is connected. The issue is not that $ (-1,1) $ fails to be connected. Rather, it is that it cannot be contained in $ B $ when $ B $ is separated in this way.

Proof

Assumptions

Let $ A $ and $ B $ be subsets of a topological space $ X $.

$$ A \subset X \quad \text{and} \quad B \subset X $$

Assume that:

$ A $ is connected
$ A \subset B $
$ B_1 $ and $ B_2 $ form a separation of $ B $ in $ X $

Claim

Then $ A $ is a subset of either $ B_1 $ or $ B_2 $:

$$ A \subset B_1 \quad \text{or} \quad A \subset B_2 $$

Proof

By assumption, $ B_1 $ and $ B_2 $ form a separation of $ B $ in $ X $. Consequently, the following properties hold:

$ B_1 \cap B_2 = \varnothing $, that is, $ B_1 $ and $ B_2 $ are disjoint
$ B = B_1 \cup B_2 $, that is, their union is all of $ B $
$ B_1 $ and $ B_2 $ are open in the subspace topology on $ B $

Suppose, for the sake of contradiction, that neither $ A \subset B_1 $ nor $ A \subset B_2 $ holds. In other words, assume that $ A $ is not entirely contained in either $ B_1 $ or $ B_2 $.

$$ A \cap B_1 \neq \varnothing \qquad \text{and} \qquad A \cap B_2 \neq \varnothing $$

Since $ A \subset B $, it follows that:

$$ A = A \cap B = A \cap (B_1 \cup B_2) = (A \cap B_1) \cup (A \cap B_2) $$

Because $ B_1 $ and $ B_2 $ are disjoint, the sets $ A \cap B_1 $ and $ A \cap B_2 $ are likewise disjoint.

Therefore, the sets $ A \cap B_1 $ and $ A \cap B_2 $ are disjoint, nonempty, and open in the subspace topology on $ A $. Hence, they form a separation of $ A $ in $ X $.

This contradicts the assumption that $ A $ is connected.

It follows that the assumption is false, and therefore the desired conclusion holds:

$$ A \subset B_1 \quad \text{or} \quad A \subset B_2 $$

This completes the proof.

And so on.