Conditional Probability

Conditional probability measures the likelihood of event E (the conditioned event) given that event A (the conditioning event) has already occurred.

It is also known as posterior probability.

If the events are dependent, the conditional probability P(E|A) is calculated using the formula:

$$ P(E|A) = \frac{P(E \cap A)}{P(A)} $$

Where E represents the conditioned event, and A is the conditioning event.

• P(E|A) is the conditional probability of E given A.
• P(E∩A) represents the probability that both E and A occur (joint probability).
• P(A) is the probability of the conditioning event A.

Conditional probability adjusts the likelihood of event E by taking into account the additional information that event A has already occurred.

Note. The probability of the conditioning event P(A) must be greater than zero; otherwise, it would result in division by zero: $$ P(A) \ne 0 $$

If the two events are independent, the occurrence of one does not affect the probability of the other. In such cases, the probability of E remains unchanged.

$$ P(E|A) = P(E) $$

Example. Here are some practical examples:


• The probability of rain (event E) given that it rained yesterday (event A).
• The probability of failing an exam (event E) if a student did not study enough (event A).
• The probability of a heart attack (event E) given that the patient is elderly (event A).

A Practical Example

Example 1

What is the probability of drawing an ace from a deck of cards, knowing that the drawn card is a heart?

In this case, the conditioned event E is "drawing an ace," while the conditioning event A is "drawing a heart card."

In a standard deck of playing cards, there are 52 cards in total, including 4 aces and 13 hearts (one of which is the ace of hearts).

The probability of drawing a heart is P(A)= 13/52.

$$ P(A) = \frac{13}{52} $$

The probability of drawing an ace given that the card is a heart is P(E∩A)=1/52, as there is only one ace of hearts in the deck.

$$ P(E∩A) = \frac{1}{52} $$

Now, using the formula for conditional probability:

$$ P(E|A) = \frac{P(E \cap A)}{P(A)} $$

$$ P(E|A) = \frac{ \frac{1}{52} }{ \frac{13}{52} } $$

$$ P(E|A) = \frac{1}{52} \cdot \frac{52}{13} $$

$$ P(E|A) = \frac{1}{13} $$

$$ P(E|A) \approx 0.0769 $$

So, the probability of drawing an ace, given that the card drawn is a heart, is approximately 0.0769 or $7.6\%$.

This means that, if you know the drawn card is a heart, there is a 7.6% chance that it is also an ace.

Example 2

70% of the population wears pants, while 30% wears skirts.

The probability that a random passerby is wearing pants is P(E)=70%.

$$ P(E) = 70\% $$

Where E is the event that a person wearing pants passes by.

Given that the next passerby is a woman (conditioning event A), we need to calculate the conditional probability P(E|A) of event E given A.

$$ P(E|A) = \frac{P(E \cap A)}{P(A)} $$

The probability of encountering a woman is 60%, as 6 out of 10 people are women: P(A)=0.6.

The probability of encountering a woman wearing pants (E⋂A) is 30%, as 3 out of 10 are women wearing pants: P(E⋂A)=0.3.

So, the conditional probability is:

$$ P(E|A) = \frac{0.3}{0.6} = 0.50 $$

The probability that the next passerby is wearing pants (event E), given that the person is a woman (event A), is 50%.

Example 3

Rolling two dice results in a sample space S consisting of 36 possible outcomes.

$$ (i,j) $$

Where i=1,2,3,4,5,6 represents the outcome of the first die, and j=1,2,3,4,5,6 represents the outcome of the second die.

$$ S = \begin{pmatrix} (1,1) & (1,2) & (1,3) & (1,4) & (1,5) & (1,6) \\ (2,1) & (2,2) & (2,3) & (2,4) & (2,5) & (2,6) \\ (3,1) & (3,2) & (3,3) & (3,4) & (3,5) & (3,6) \\ (4,1) & (4,2) & (4,3) & (4,4) & (4,5) & (4,6) \\ (5,1) & (5,2) & (5,3) & (5,4) & (5,5) & (5,6) \\ (6,1) & (6,2) & (6,3) & (6,4) & (6,5) & (6,6) \end{pmatrix} $$

If the first die shows a 4 (conditioning event A), what is the probability that the sum of the dice is 7 (conditioned event E)?

$$ P(E|A)= \frac{P(E \cap A)}{P(A)} $$

The probability P(E ∩ A) that the sum is 7 and the first die is 4 is 1/36, as the only outcome satisfying this condition is (4,3) in a sample space S with 36 total outcomes.

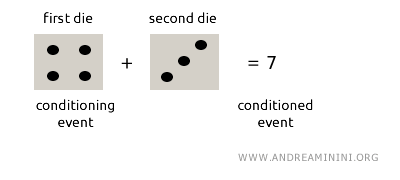
Thus, P(E ∩ A) = 1/36

$$ P(E|A)= \frac{\frac{1}{36}}{P(A)} $$

The probability of the conditioning event, which is rolling a 4 on the first die, is P(A) = 1/6, since the die has six faces.

$$ P(E|A)= \frac{\frac{1}{36}}{\frac{1}{6}} $$

Simplifying the calculation gives:

$$ P(E|A)= \frac{\frac{1}{36}}{\frac{1}{6}} = \frac{1}{36} \cdot \frac{6}{1} = \frac{1}{6} $$

Therefore, the conditional probability that the sum is 7 given that the first die shows a 4 is P(E|A) = 1/6.

And so on.