Intersection of events

The intersection of events is the event in which two or more events, defined on the same sample space, occur simultaneously. $$ E_1 \cap E_2 $$

This type of event is also referred to as a logical product and, in standard probability terminology, as a joint event.

The intersection of events makes it possible to determine the probability that several events occur at the same time.

In probability theory and statistics, events are commonly described using the language of set theory, where joint occurrences are modeled as set intersections. 

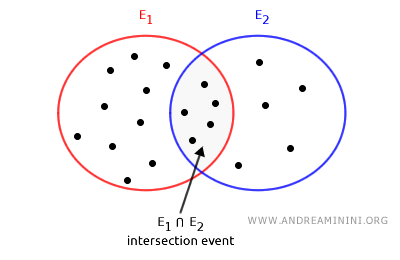
Note. Although event notation uses symbols borrowed from set theory, it does not represent actual set operations. Instead, it encodes simultaneity in the case of an intersection event, or mutually exclusive alternatives in the case of a union event.

This notation provides a clear and rigorous framework for analyzing situations in which multiple conditions must be satisfied simultaneously.

The compound probability theorem

To compute the probability of the logical product of two events \( E_1 \) and \( E_2 \), that is, the joint event \( E_1 \cap E_2 \), it is necessary to distinguish between two fundamental cases.

• Independent events
  Two events are said to be stochastically independent when the occurrence of one does not influence the probability of the other. In this case, the probability of the joint event is given by the product of the probabilities of the individual events: \[ p(E_1 \cap E_2) = p(E_1)\cdot p(E_2) \]
• Dependent events
  If two events are dependent, the occurrence of one alters the probability of the other. The probability of the joint event is obtained by multiplying the probability of the first event by the conditional probability of the second event given the first: \[ p(E_1 \cap E_2) = p(E_1)\cdot p(E_2 \mid E_1) \] This formulation is particularly useful when a direct evaluation of \( p(E_1 \cap E_2) \) is impractical, but the quantities \( p(E_1) \) and \( p(E_2 \mid E_1) \) are readily accessible.

  Note. The conditional probability \( p(E_2 \mid E_1) \) is defined as: \[ p(E_2 \mid E_1) = \frac{p(E_1 \cap E_2)}{p(E_1)} \quad \text{with } p(E_1)\neq 0 \] From this definition, the compound probability formula for dependent events follows directly: \[ p(E_1 \cap E_2) = p(E_1)\cdot p(E_2 \mid E_1) \] This expression is fully general, as it also applies to independent events. When two events are independent, the conditional probability reduces to the probability of the single event, namely \( p(E_2 \mid E_1) = p(E_2) \). Substituting into the general formula yields: \[ p(E_1 \cap E_2) = p(E_1)\cdot p(E_2) \]

What if there are more than two events?

If three events are involved, the probability of their joint occurrence is computed by applying conditional probability successively:

\[ p(E_1 \cap E_2 \cap E_3) = p(E_1)\cdot p(E_2 \mid E_1)\cdot p(E_3 \mid E_1 \cap E_2) \]

If all events are mutually independent, the formula reduces to the simple product of their probabilities:

\[ p(E_1)\cdot p(E_2)\cdot p(E_3) \]

A practical example

Consider a class of 30 students. Among them:

• 15 play soccer
• 10 swim
• 5 both play soccer and swim

Define two events, E₁ and E₂.

$$ E_1: \ \text{The student plays soccer.} $$ $$ E_2: \ \text{The student swims.} $$

The intersection of E₁ and E₂ represents the students who both play soccer and swim.

$$ E_1 \cap E_2 : \ \text{The student both plays soccer and swims.} $$

From the data provided, it follows that 5 students belong to this category.

Therefore, the joint event E₁∩E₂ occurs for these 5 students.

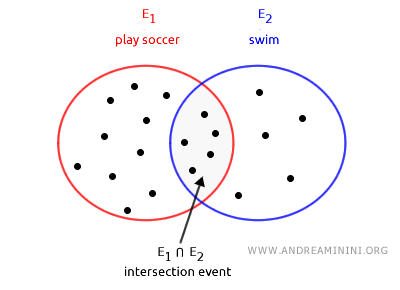
In set-theoretic terms, this corresponds to elements that belong simultaneously to both set E₁ and set E₂.

Example 2

Consider tossing a coin and rolling a die.

Define the events:

• \( E_1 \): the coin lands heads
• \( E_2 \): the die shows a 6

The two events are stochastically independent, since the outcome of the coin does not affect the outcome of the die.

The probabilities of the individual events are:

\[ p(E_1) = \tfrac{1}{2} \]

\[ p(E_2) = \tfrac{1}{6} \]

Because the events are independent, the probability of the joint event is:

\[ p(E_1 \cap E_2) = p(E_1)\cdot p(E_2) \]

\[ p(E_1 \cap E_2) = \tfrac{1}{2}\cdot \tfrac{1}{6} = \tfrac{1}{12} = 0.083 = 8.3 \% \]

So, the probability is 8.3%.

Example 3

Consider an urn containing 3 red balls and 2 blue balls.

What is the probability of drawing two red balls in succession without replacement?

In this situation, the first draw affects the probability of the second draw, because the ball is not returned to the urn. The events are therefore dependent.

Define the events:

• \( E_1 \): the first ball drawn is red
• \( E_2 \): the second ball drawn is red

The probability of the first event is \( \frac{3}{5} \), since initially there are 3 red balls out of 5.

\[ p(E_1) = \tfrac{3}{5} \]

If the first ball is red, 2 red balls remain out of 4 total balls.

Therefore, the conditional probability of the second event \( E_2 \) given the first event \( E_1 \) is:

\[ p(E_2 \mid E_1) = \tfrac{2}{4} = \tfrac{1}{2} \]

The probability that both balls drawn are red is:

\[ p(E_1 \cap E_2) = p(E_1)\cdot p(E_2 \mid E_1) \]

\[ p(E_1 \cap E_2)  = \tfrac{3}{5}\cdot \tfrac{1}{2} = \tfrac{3}{10} = 0.3 = 30 \% \]

Overall, the probability of drawing two red balls in succession is 30%.

Note. In this case, the product of the individual probabilities cannot be used, because the first draw alters the probability of the second.

And so on.