Probability of events
To each event E in a sample space S, a probability P(E) is assigned.
When an experiment is repeated many times under identical conditions, an event tends to occur with a stable empirical relative frequency, which is interpreted as its probability P(E).
The probability assigned to an event is not arbitrary. It must satisfy a set of fundamental axioms.
- Axiom 1
The probability of an event is a real number between 0 and 1. $$ 0 \le P(E) \le 1 $$ - Axiom 2
The total probability associated with the entire sample space is equal to 1. $$ P(S)=1 $$ - Axiom 3
If the sample space is a finite collection of mutually exclusive events, meaning that if one event E1 occurs none of the others can occur, then the probability that at least one of them occurs is equal to the sum of their probabilities. $$ P( U_{i=1}^n E_i ) = \sum_{i=1}^n P(E_i) $$ When two events are not mutually exclusive, they may occur at the same time. In that case, the probability that one event or the other occurs must be computed using a corrected formula. $$ P(E∪F) = P(E)+P(F)-P(E⋂F) $$Example. When rolling a die, event E occurs if the outcome is 2, while event F occurs if the outcome is 1. The corresponding probabilities are $ P(E)=\frac16 $ and $ P(F)=\frac16 $. The two events are mutually exclusive. Therefore, the probability of obtaining either a 1 or a 2 is $$ P(E)+P(F)=\frac16+\frac16=\frac13 $$
Total probability theorem
The probability of the logical sum, that is, the union, of two events \( E_1 \) and \( E_2 \) is equal to the sum of the probabilities of the individual events, minus the probability of their intersection. \[ p(E_1 \cup E_2) = p(E_1) + p(E_2) - p(E_1 \cap E_2) \]
The term \( p(E_1 \cap E_2) \) is subtracted because, when \( p(E_1) \) and \( p(E_2) \) are added, outcomes common to both events would otherwise be counted twice.
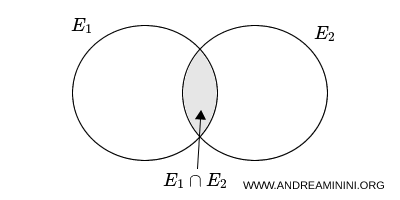
Special case: incompatible events
Two events are said to be incompatible, or mutually exclusive, if they cannot occur at the same time. In this situation, their intersection is the empty set:
\[ E_1 \cap E_2 = \emptyset \]
As a consequence, the probability of the intersection is zero.
\[ p(E_1 \cap E_2) = 0 \]
The general formula therefore simplifies to:
\[ p(E_1 \cup E_2) = p(E_1) + p(E_2) \]
Note. This result holds for any pair of events. The case of incompatible events does not introduce a new theorem. It follows directly from the general formula when no outcomes are shared by \( E_1 \) and \( E_2 \).
Examples
Example 1 (incompatible events)
A six-sided die is rolled and two events are considered.
- \( E_1 = \) “the outcome is 1”
- \( E_2 = \) “the outcome is 6”
The two events are incompatible because they cannot occur simultaneously.
The probabilities are:
\[ p(E_1) = \frac{1}{6}, \quad p(E_2) = \frac{1}{6} \]
Since \( E_1 \cap E_2 = \emptyset \), it follows that:
\[ p(E_1 \cup E_2) = p(E_1) + p(E_2) = \frac{1}{6} + \frac{1}{6} = \frac{2}{6} = \frac{1}{3} = 0.\overline{3} \]
The probability that at least one of the two events occurs is 0.33, that is, approximately 33.3%.
In this case, the result coincides with the simple sum of the individual probabilities because the events cannot occur together and the probability of their intersection is zero.
Example 2 (compatible events)
A six-sided die is rolled and the following two events are considered:
- \( E_1 = \) “the outcome is an even number”
- \( E_2 = \) “the outcome is greater than 3”
The corresponding outcome sets are:
- Even numbers: \( \{ 2,4,6 \} \)
- Numbers greater than 3: \( \{ 4,5,6 \} \)
Their intersection is:
\[ E_1 \cap E_2 = \{ 4,6 \} \]
The probabilities are:
\[ p(E_1) = \frac{3}{6}, \quad p(E_2) = \frac{3}{6}, \quad p(E_1 \cap E_2) = \frac{2}{6} \]
Applying the general formula, we obtain:
\[ p(E_1 \cup E_2) = \frac{3}{6} + \frac{3}{6} - \frac{2}{6} = \frac{4}{6} = \frac{2}{3} =0.\overline{6} \]
Here, the intersection must be subtracted because the shared outcomes \( \{ 4,6 \} \) would otherwise be counted twice.
Therefore, the probability that at least one of the two events occurs is 0.66, or approximately 66.6%.
Example 3
Thirty-five percent of the population owns a car (event E), 10% owns a motorcycle (event F), and 5% own both a car and a motorcycle (E ⋂ F).
What percentage of the population owns neither a car nor a motorcycle?
First, compute the percentage of individuals who own at least one car or one motorcycle.
$$ P(E ∪ F) = P(E)+P(F)-P(E ⋂ F) = 0.35+0.10-0.05 = 0.40 $$
Thus, 40% of the population owns at least one car or one motorcycle.
Consequently, 60% of the population owns neither a motorcycle nor a car.
$$ 1 - 0.4 = 0.6 $$
Remarks
The following points highlight some useful consequences of the preceding results.
- Probability of the union of three events
For three events \( E_1 \), \( E_2 \), and \( E_3 \), the probability of their union accounts for all possible overlaps among the events. The relation is given by: \[ \begin{aligned} p(E_1 \cup E_2 \cup E_3) &= p(E_1) + p(E_2) + p(E_3) \\ &\quad - p(E_1 \cap E_2) - p(E_1 \cap E_3) - p(E_2 \cap E_3) \\ &\quad + p(E_1 \cap E_2 \cap E_3) \end{aligned} \] The terms \( p(E_1) + p(E_2) + p(E_3) \) represent the probabilities of the individual events. The pairwise intersections are subtracted because they are counted twice. The triple intersection $ p(E_1 \cap E_2 \cap E_3) $ is added back because it had been subtracted three times in the earlier steps.
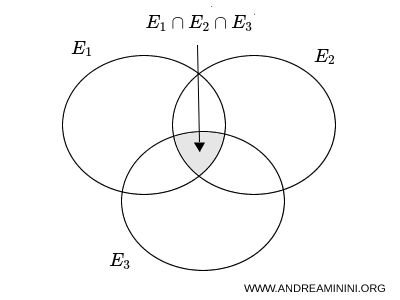
Note. The underlying principle is the same as in the two-event case. As the number of events increases, careful correction for overlapping regions becomes essential in order to avoid overcounting.
- Given an event E, the probability that it does not occur is obtained by considering its complement Ec. The complementary event Ec consists of all outcomes in the sample space that are not contained in E. Therefore, the probability that E does not occur is equal to one minus the probability of E. $$ P(E^c) = 1 - P(E) $$
Example. If the sample space of a die roll consists of six equally likely outcomes, one for each face, and event E corresponds to rolling a 2 with probability P(E)=1/6, then the probability that E does not occur is P(Ec)=1-1/6=5/6.
And so on.
