Sum Rule for Compatible Events
The sum rule for compatible events states that the probability p(E1∪E2) of either of two compatible events occurring is equal to the sum of the probabilities of each event individually, minus the probability that both events occur at the same time. $$ p(E1∪E2) = p(E1) + p(E2) - p(E1∩E2) $$
Where:
- p(E1) is the probability of event E1 occurring
- p(E2) is the probability of event E2 occurring
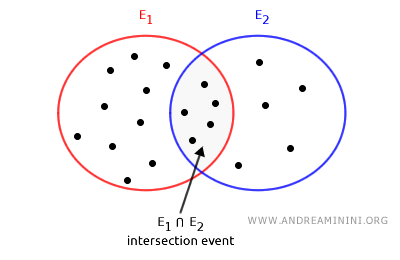
- p(E1∩E2) is the intersection of the two events, or the probability that both events occur simultaneously.
This theorem provides a way to calculate the probability p(E1∪E2) that at least one of two events occurs (the union of events), when E1 and E2 can happen at the same time.
What are compatible events?
Two or more events are considered compatible events (or not mutually exclusive) if they can occur simultaneously.
Proof. The proof of the sum rule for compatible events is based on the fact that when counting the probability of each event individually, the intersection of events E1∩E2 is counted twice—once in p(E1) and once in p(E2). To correct this, we subtract the probability of the intersection once to avoid double counting.
A Practical Example
Let's consider a deck of 52 cards and two events, E1 and E2:
E1: "drawing an ace"
E2: "drawing a heart"
These two events are compatible because they can happen simultaneously, such as drawing the ace of hearts.
To calculate the probability that at least one of these events occurs, we use the sum rule for compatible events.
$$ p(E1∪E2)=p(E1)+p(E2) - p(E1∩E2) $$
Since there are 4 aces in a deck of 52 cards, the probability of drawing an ace (event E1) is 4/52.
$$ p(E1) = \frac{4}{52} $$
There are 13 hearts in the deck, so the probability of drawing a heart (event E2) is 13/52.
$$ p(E2) = \frac{13}{52} $$
Next, we calculate the probability of drawing a card that is both an ace and a heart, p(E1∩E2).
Since there is only one ace of hearts in the deck, the probability is 1/52.
$$ p(E1∩E2) = \frac{1}{52} $$
Now, we substitute these probabilities into the sum rule for compatible events.
$$ p(E1∪E2)=p(E1)+p(E2) - p(E1∩E2) $$
$$ p(E1∪E2)= \frac{4}{52} + \frac{13}{52} - \frac{1}{52} $$
$$ p(E1∪E2)= \frac{4+13-1}{52} $$
$$ p(E1∪E2)= \frac{16}{52} $$
This simplifies to
$$ p(E1∪E2)= \frac{4}{13} $$
So, the probability of drawing either an ace or a heart is 4/13, or approximately 30.77%.
Additional Notes
Here are a few additional points on the sum rule for compatible events:
- The sum rule also applies to incompatible events
The sum rule can be applied to both compatible and incompatible events. However, for incompatible events, the probability of the intersection is zero, as the intersection event E1∩E2=Ø is an empty set because the two events cannot occur at the same time. In this case, the formula simplifies to just the sum of the individual probabilities, without needing to subtract the intersection term. $$ p(E1∪E2)=p(E1)+p(E2) - p(E1∩E2) $$ $$ p(E1∪E2)=p(E1)+p(E2) - p(Ø) $$ $$ p(E1∪E2)=p(E1)+p(E2) - 0 $$ $$ p(E1∪E2)=p(E1)+p(E2) $$
And so on.
