Events in Probability Theory
An event is an occurrence described by a statement that may or may not happen.
In probability theory, events are usually grouped into three main categories.
- Certain events
These events occur with complete certainty. For example, when you roll a standard six-sided die, the result is guaranteed to be a number between 1 and 6. - Impossible events
These events cannot occur under any circumstances. For instance, rolling a 7 on a six-sided die is impossible. - Random events
These events are genuinely uncertain. Their occurrence depends on chance, and no single outcome can be predicted with certainty. For example, rolling a die may produce a 3, but there is no guarantee it will.
Random events lie at the heart of probability theory because they make it possible to formalize and measure probability.
A random event can be understood as the outcome of a stochastic procedure, known as a random experiment. Each individual outcome is called a sample point or elementary event.
The complete set of all possible outcomes is referred to as the sample space, or outcome space.
Formally, an event \( E \) is any subset of the sample space. It includes exactly the outcomes that satisfy the condition defining the event.
Example of an Event
When rolling a die, the sample space is a finite set containing 6 elements (possible outcomes):
$$ S = \{ 1, 2, 3, 4, 5, 6 \} $$
An example of an event E is rolling an even number.
The event E is a set containing three outcomes:
$$ E = \{ 2, 4, 6 \} $$
Another event is rolling an odd number.
Event D is also a set with three outcomes:
$$ D = \{ 1, 3, 5 \} $$
Yet another event is rolling a number less than 3.
Event F is a set with two outcomes:
$$ F = \{ 1, 2 \} $$
These three events, D, E, and F, can be represented using a Venn diagram.
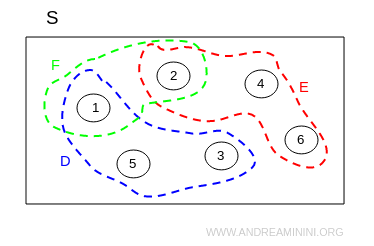
Here, S represents the sample space, and the numbered circles represent the outcomes.
Empty Event
If an event contains no outcomes, it is called an empty event and is denoted by the symbol for the empty set.
For instance, the event F, representing negative numbers in a dice roll, is an empty event because it contains no possible outcomes.
$$ F = \{ \} = Ø $$
Subset and Equality Relations
If all outcomes of event A are also outcomes of event B, we say that A is a subset of B: $$ A ⊂ B $$
The two events are in a subset relationship.
This means that if A occurs, then B will also occur.
Example: Event G consists of all outcomes where the dice roll results in a 2: $$ G = \{ 2 \} $$ Event G is a subset of event E (the even numbers): $$ G ⊂ E $$ that is, $$ \{ 2 \} ⊂ \{ 2, 4, 6 \} $$ As shown in this Venn diagram:
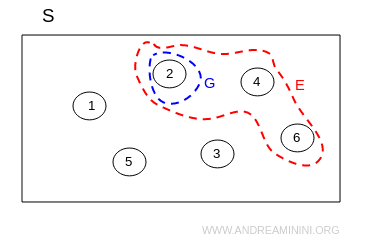
If both events are subsets of each other, this means the two sets have the same outcomes:
$$ A ⊂ B, A ⊃ B \Leftrightarrow A = B $$
In this case, the two events are in an equality relationship.
Union and Intersection of Events
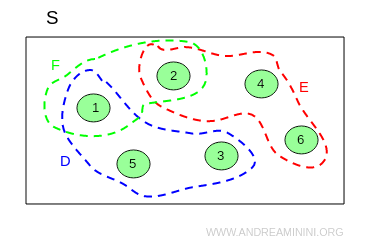
The union of events E and D includes all the outcomes from both E and D. This occurs when at least one of the events E or D happens:
$$ E \cup D = \{ 2, 4, 6 \} \cup \{ 1, 3, 5 \} = \{ 1, 2, 3, 4, 5, 6 \} $$
In this case, the union is equivalent to the entire sample space.
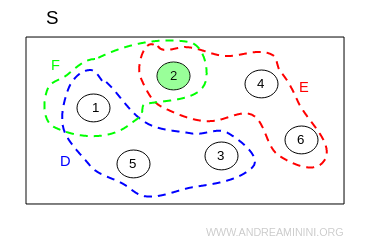
The intersection of events E and F consists of the outcomes that are common to both E and F:
$$ E \cap F = \{ 2, 4, 6 \} \cap \{ 1, 2 \} = \{ 2 \} $$
This can be visualized as follows:
If the intersection of two events is empty, it means the events cannot occur simultaneously. Such events are called disjoint events or mutually exclusive events:
$$ E \cap D = \{ 2, 4, 6 \} \cap \{ 1, 3, 5 \} = \{ \} $$
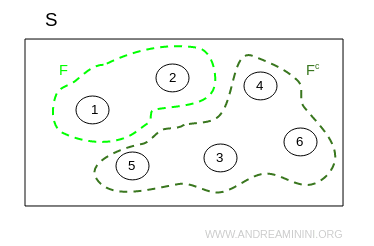
Complement of an Event
The complement Fc of an event F is the set of outcomes that do not satisfy F.
Example:
If event F is the set of numbers less than three when rolling a die:
$$ F = \{ 1, 2 \} $$
its complement is the set of numbers greater than two:
$$ F^c = \{ 3, 4, 5, 6 \} $$
This can be shown in a Venn diagram:
And so on.
