Complementary Event

In probability and statistics, a complementary event E' represents the opposite outcome of a given event E.

If E is a specific event, its complementary event (or complement) is denoted by \(E'\) or \(E^{c}\) and occurs only when \(E\) does not occur.

For example, if we consider rolling a six-sided die and event \(E\) is "rolling an even number", then the complementary event \(E'\) would be "rolling an odd number".

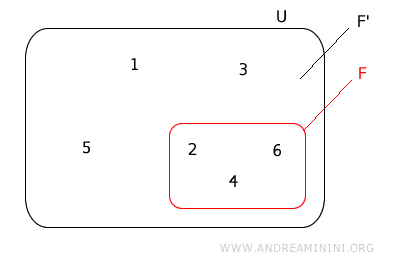
In set theory terms, if U represents the universal set containing all elements, and F is the set of outcomes that favor event E, then F' is the complementary set U\F.

$$ F' = U \text{ \ } F $$

This means that F' includes all elements of U that are not in F.

For example, here's a representation of event E ("rolling an even number") and its complement E' using Euler-Venn diagrams.

A fundamental theorem in probability theory states that the sum of the probability of an event and its complementary event is always equal to 1: $$ p(E) + p(E') = 1 $$

This theorem is very useful because it provides a direct method to calculate the probability of an event if we know the probability of its complement.

Proof. We start with the sum of the probabilities of event E and its complement E': $$ p(E) + p(E') $$ The probability p(E) = f/n is the ratio between favorable outcomes (f) and the total number of outcomes (n). $$ p(E) + p(E') = \frac{f}{n} + p(E') $$ The probability p(E') = (n-f)/n of the complementary event is the ratio between unfavorable outcomes (n-f) and the total number of outcomes (n): $$ p(E) + p(E') = \frac{f}{n} + \frac{n-f}{n} $$ After simplifying, we get n/n, which equals 1. $$ p(E) + p(E') = \frac{f+n-f}{n} = \frac{n}{n} = 1 $$

A Practical Example

Let's consider the event E = "rolling a number greater than 2" with a six-sided die.

The sample space is:

$$ U = \{ 1,2,3,4,5,6 \} $$

The set of favorable outcomes is:

$$ F = \{ 3,4,5,6 \} $$

We calculate the ratio between the number of elements in set F and set U to determine the probability of event E:

$$ p(E) = \frac{|F|}{|U|} = \frac{4}{6} = 0.66 $$

The cardinality of set F is |F| = 4 since it contains 4 elements, while the cardinality of set U is |U| = 6.

Therefore, the probability of rolling a number greater than 2 (event E) is approximately 0.67, or 67%.

The complementary event E' represents the opposite scenario: "rolling a number less than or equal to 2".

In this case, we can skip calculating the probability of E' directly, since we already know the probability p(E) = 0.67 of event E and can find E's complement by subtraction.

Knowing that, according to the probability theorem, the sum of the probabilities of an event E and its complement E' equals 1:

$$ p(E) + p(E') = 1 $$

We can derive the probability of p(E'):

$$ p(E') = 1 - p(E) $$

$$ p(E') = 1 - 0.67 $$

$$ p(E') = 0.33 $$

So, we've determined the probability of E' by subtraction, without having to calculate it as a ratio of favorable to total outcomes.

The probability of rolling a number less than or equal to 2 is approximately 0.33, or 33%.

And so on.