Random Events

A random event is a phenomenon or outcome that cannot be predicted with complete certainty. It's also referred to as a chance event.

Random events are closely related to the concept of probability and are encountered in many aspects of everyday life.

In mathematics and statistics, the notion of randomness is fundamental for studying probability and random phenomena.

For example, rolling a die or flipping a coin are random events because the outcome cannot be known beforehand.

Characteristics of Random Events

Random events have the following characteristics:

• Unpredictability
  The outcome of a random event cannot be predicted with certainty before it occurs, even if all initial conditions are known.
• Repeatability
  When a random event is repeated multiple times under the same conditions, it may follow a specific probability distribution.

  Example. If I flip a coin many times, the number of heads (or tails) will tend to approach 50% over time.

• Indeterminism
  Unlike deterministic phenomena, where the outcome can be predicted precisely given a set of initial conditions, random events are fundamentally unpredictable.

A Practical Example

Consider rolling a six-sided die, a classic example of a random event.

When I roll the die, there are six possible outcomes: \(1, 2, 3, 4, 5, 6\). The random event is the number that appears.

This example meets all the characteristics of random events:

• Unpredictability: I can’t know for sure which number will come up before rolling the die, even if I know all the initial conditions, like the height or force of the roll.
• Repeatability: if I roll the die many times, each number has the same probability of occurring (around \( \frac{1}{6} \)), and the distribution of results will gradually align with this probability.
• Indeterminism: even if the experiment is repeated under identical conditions, the result remains unpredictable and cannot be determined precisely.

Thus, rolling a die is a random phenomenon where the result of each individual roll cannot be predicted with certainty.

However, it is still possible to make probabilistic predictions about the overall outcomes over a large number of rolls.

Random Events in Science

Random events are a key subject in statistics, particularly in probability theory.

Today, randomness is a fundamental concept in both pure and applied sciences.

For example, the orbit of an electron around an atom cannot be predicted with absolute certainty. Therefore, atomic orbitals are not fixed paths but rather regions (clouds) around the atom where the electron is most likely to be found.

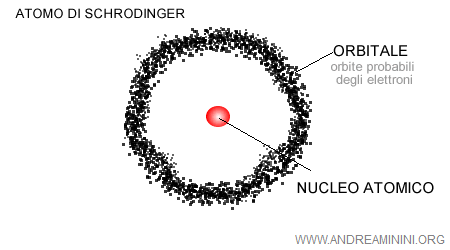
In 1926, the Austrian physicist Erwin Schrödinger developed a specific equation (known as the Schrödinger equation) to calculate the most probable orbit of electrons. This marked a shift away from scientific determinism and towards a probabilistic approach to studying natural phenomena.

Even though random events are inherently unpredictable, understanding and modeling them have led to significant advancements in a wide range of fields.

And so on.