Glide Reflection

A glide reflection is a geometric transformation of the plane that combines a reflection across a line $r$ with a translation $T_{\vec{v}}$ along a vector $\vec{v}$ parallel to that line. $$ G = T_{\vec{v}} \circ S_r $$

A glide reflection is an isometry, meaning it preserves distances between points.

Still, it cannot be reduced to any single basic transformation on its own.

It is not a pure reflection, because no line remains pointwise fixed: every point in the plane is displaced.

Nor is it a simple translation, since the reflection necessarily reverses the orientation of the figure.

Note. There are a few straightforward exceptions. If the translation vector is zero ($\vec{v}=0$), the glide reflection reduces to a reflection. If the reflection is omitted, what remains is just a translation.

A worked example

Consider the Cartesian plane, a reflection, and a translation:

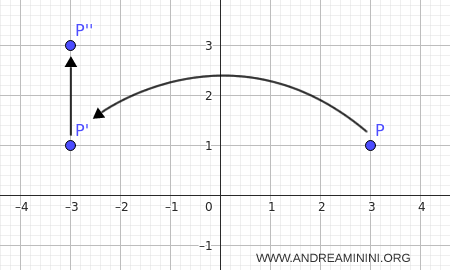
• The reflection is across the line $r: x=0$, i.e. the $y$-axis.
• The translation is defined by the vector $\vec{v} = (0,2)$, which is parallel to $r$.

Take the point $P(3,1)$.

Reflecting across $r$ gives $P'(-3,1)$.

Applying the translation $\vec{v}$ then yields $P''=(-3,1+2) = (-3,3)$.

Thus, under the glide reflection, $P$ is mapped to $P''$.

Geometrically, a glide reflection can be visualized as a “reflected slide”: first reflect the figure across a line, then shift it along that line.

Further notes

Some additional remarks on glide reflections:

• No fixed points
  Unlike a reflection, where points on the axis remain unchanged, a glide reflection has no fixed points at all. Every point of the plane is displaced. The only element preserved globally is the axis of reflection, which is mapped onto itself, even though none of its individual points remain fixed.

And so forth.