Sample Variance
The sample variance quantifies the variability of the elements within a statistical sample relative to their mean. $$ \sigma^2 = \frac{1}{n-1} \cdot \sum_{i=1}^n (x_i - \mu)^2 $$ Here, n is the number of elements in the sample, and μ represents the sample mean.
Sample variance provides an estimate of the population variance based on the variance calculated from a random sample drawn from that population.
It is particularly useful for measuring variability when it’s impractical or costly to compute the population variance directly.
For example, it’s used in cases where measuring variability would require destroying the sample.
How is it different from population variance? Population variance is calculated from the entire population, while sample variance is calculated from just a subset. The formula for sample variance uses a denominator that is reduced by one (n-1), where n is the size of the sample.
A Practical Example
Let’s say I need to calculate the average height of students enrolled in a high school, where the total population consists of 1,000 students.
To avoid measuring the entire population, I calculate the average height using a representative sample of 10 students (1% of the population).
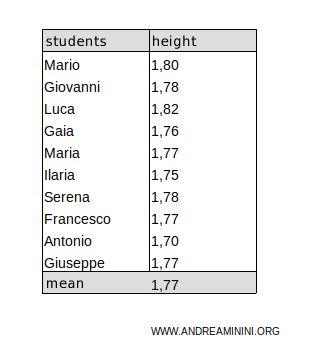
The average height in the sample is 1.77 meters.
$$ \mu = 1.77 $$
Given that the sample mean is μ=1.77 and the sample size is n=10, I can calculate the sample variance as follows:
$$ \sigma^2 = \frac{1}{n-1} \cdot \sum_{i=1}^n (x_i - \mu)^2 $$
$$ \sigma^2 = \frac{1}{10-1} \cdot \sum_{i=1}^n (x_i - 1.77)^2 $$
$$ \sigma^2 = \frac{1}{9} \cdot [ ( 1.80-1.77)^2+( 1.78-1.77)^2+( 1.82-1.77)^2+ ( 1.76-1.77)^2+ \\ \ \ \ \ +( 1.77-1.77)^2+( 1.75-1.77)^2+( 1.78-1.77)^2+ \\ \ \ \ \ + ( 1.77-1.77)^2+( 1.70-1.77)^2+( 1.77-1.77)^2 ] $$
$$ \sigma^2 = \frac{1}{9} \cdot [ ( 0.03)^2+( 0.01)^2+( 0.05)^2+( 0.01)^2+( 0)^2+ \\ \ \ \ \ +( -0.02)^2+( 0.01)^2+( 0)^2+( -0.07)^2+(0)^2 ] $$
$$ \sigma^2 = \frac{1}{9} \cdot [ 0.0009+ 0.0001+0.0025+0.0001+0.0004+0.0001+0.0049 ] $$
$$ \sigma^2 = \frac{1}{9} \cdot 0.009 $$
So, the sample variance is σ2=0.001
$$ \sigma^2 = 0.001 $$
This result provides an estimate of the variance for the sample mean μ=1.77 across the entire population of 1,000 students.
And that’s the process.
