Variance

Variance is a measure of the spread or dispersion in a statistical distribution, calculated as the average of the squared deviations from the arithmetic mean (μ). $$ \sigma^2 = \frac{1}{n} \cdot \sum_{i=1}^n (x_i - \mu )^2 $$

For frequency distributions, the variance formula is slightly different:

$$ \sigma^2 = \frac{1}{\sum_i^k n_i} \cdot \sum_{i=1}^k (x_i - \mu )^2 \cdot n_i $$

Here, μ is the arithmetic mean, and n_i represents the frequencies.

Variance is based on the principle that the sum of the squared deviations from the mean is minimized—it’s the smallest possible value.

If you were to sum the squared deviations from a value other than the mean, the result would be larger.

Note. Variance is expressed in the square of the unit of measurement for the data. For instance, if the data is measured in meters, the variance will be in square meters. Therefore, variance and the data distribution cannot be represented on a single diagram.

A practical example

Example 1

Let’s consider a data set with n=6 elements:

$$ 1 \ , \ 5 \ , \ 7 \ , \ 3 \ , \ 6 \ , \ 8 $$

The arithmetic mean of this data set is μ=5:

$$ \mu = \frac{1+5+7+3+6+8}{6 } = \frac{30}{6 } = 5 $$

To measure the dispersion around the mean, we calculate the variance:

$$ \sigma^2 = \frac{1}{n} \cdot \sum_{i=1}^n (x_i - \mu )^2 $$

Given n=6 and μ=5, we have:

$$ \sigma^2 = \frac{1}{6} \cdot \sum_{i=1}^n (x_i - 5 )^2 $$

Using the values x₁=1, x₂=5, x₃=7, x₄=3, x₅=6, x₆=8, the calculation becomes:

$$ \sigma^2 = \frac{1}{6} \cdot [ (1- 5 )^2+(5- 5 )^2+(7- 5 )^2+(3- 5 )^2+(6- 5 )^2+(8- 5 )^2] $$

$$ \sigma^2 = \frac{1}{6} \cdot [ (-4 )^2+(0 )^2+(2)^2+(-2)^2+(1)^2+(3)^2] $$

$$ \sigma^2 = \frac{1}{6} \cdot [ 16+0+4+4+1+9] $$

$$ \sigma^2 = \frac{34}{6} $$

Therefore, the variance of this data set is σ^₂=5.66

$$ \sigma^2 = 5.66 $$

Example 2

Now, let’s look at this frequency distribution:

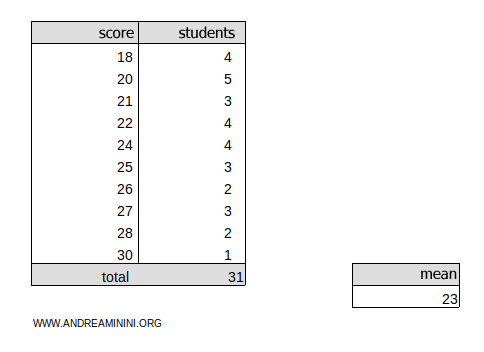
The weighted arithmetic mean of the data is μ=23

To calculate the variance in this case, we use the frequency distribution formula:

$$ \sigma^2 = \frac{1}{\sum_i^k n_i} \cdot \sum_{i=1}^k (x_i - \mu )^2 \cdot n_i $$

There are k=10 classes in the table, and the mean is μ=23:

$$ \sigma^2 = \frac{1}{\sum_i^{10} n_i} \cdot \sum_{i=1}^{10} (x_i - 23 )^2 \cdot n_i $$

The sum of the frequencies is Σn_i=31

$$ \sigma^2 = \frac{1}{31} \cdot \sum_{i=1}^{10} (x_i - 23 )^2 \cdot n_i $$

We now calculate the squared deviations for each value x₁=18, x₂=20, x₃=21, x₄=22, x₅=24, x₆=25, x₇=26, x₈=27, x₉=28, x₁₀=30 from the weighted mean μ=23:

$$ \sigma^2 = \frac{(18 - 23 )^2 \cdot 4 + (20 - 23 )^2 \cdot 5 + (21 - 23 )^2 \cdot 3 + (22 - 23 )^2 \cdot 4 + (24 - 23 )^2 \cdot 4 + \\ + (25 - 23 )^2 \cdot 3 + (26 - 23 )^2 \cdot 2 + (27 - 23 )^2 \cdot 3 + (28 - 23 )^2 \cdot 2 + (30- 23 )^2 \cdot 1 }{31} $$

$$ \sigma^2 = \frac{(-5)^2 \cdot 4 + (-3)^2 \cdot 5 + (-2)^2 \cdot 3 + (-1)^2 \cdot 4 + (1)^2 \cdot 4 + \\ + (2)^2 \cdot 3 + (3)^2 \cdot 2 + (4)^2 \cdot 3 + (5)^2 \cdot 2 + (7)^2 \cdot 1 }{31} $$

$$ \sigma^2 = \frac{25 \cdot 4 +9 \cdot 5 + 4 \cdot 3 +1 \cdot 4 + 1 \cdot 4 +4 \cdot 3 + 9 \cdot 2 + 16 \cdot 3 + 25 \cdot 2 + 49 \cdot 1 }{31} $$

$$ \sigma^2 = \frac{100 +45 + 12 +4 + 4 +12 + 18 + 48 + 50+ 49 }{31} $$

$$ \sigma^2 = \frac{342}{31} $$

So, the variance of this frequency distribution is σ^₂=11.03

$$ \sigma^2 = 11.03 $$

Key points to note

Here are some important notes about variance:

• Variance uses a different unit of measurement than the observed data
  Variance is measured in the square of the unit of the observed phenomenon. For example, if the data is in meters (m), the variance is in square meters (m²). Because of this, you can’t compare or plot variance and the data on the same graph or chart.
• An alternative method to calculate variance
  You can also calculate variance as the difference between the square of the quadratic mean (μ_q) and the square of the arithmetic mean (μ): $$ \sigma^2 = \mu_q^2 - \mu^2 $$ Alternatively, variance can be found by subtracting the square of the arithmetic mean (μ²) from the arithmetic mean of the squared values (x₁²,x₂²,...,x_n²)/n: $$ \sigma^2 = \frac{x_1^2+x_2^2+...+x_n^2}{n} - \mu^2 $$
  

  Example. Let’s go back to the previous example distribution: $$ 1 \ , \ 5 \ , \ 7 \ , \ 3 \ , \ 6 \ , \ 8 $$ We already know that the arithmetic mean is μ=5 and the variance is σ²=5.66. Now, let’s calculate the quadratic mean: $$ \mu_q = \sqrt{ \frac{1^2+5^2+7^2+3^2+6^2+8^2}{6} } $$ $$ \mu_q = \sqrt{ \frac{1+25+49+9+36+64}{6} } $$ $$ \mu_q = \sqrt{ \frac{184}{6} } = \sqrt{ 30.66} = 5.538 $$ Now that we know the arithmetic mean (μ=5) and the quadratic mean (μ_q=5.538), we can calculate the variance by finding the difference between the square of the quadratic mean and the square of the arithmetic mean: $$ \sigma^2 = \mu_q^2 - \mu^2 $$ $$ \sigma^2 = 5.538^2 - 5^2 $$ $$ \sigma^2 = 30.66 - 25 $$ $$ \sigma^2 = 5.66 $$ As expected, the result is the same. The variance of the distribution is σ²=5.66.

  Proof. The formula for variance is: $$ \sigma^2 = \frac{1}{n} \cdot \sum_{i=1}^n (x_i - \mu )^2 $$ Expanding the square term: $$ \sigma^2 = \frac{1}{n} \cdot \sum_{i=1}^n (x_i^2 -2 x_i \mu + \mu^2) $$ Applying properties of summation: $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - \sum_{i=1}^n 2 x_i \mu + \sum_{i=1}^n \mu^2 \ ] $$ Since 2μ is constant, we factor it out of the second summation: $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - 2 \mu \sum_{i=1}^n x_i + n \mu^2 \ ] $$ The third summation simplifies to Σμ²=nμ²: $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - 2 \mu \cdot ( \sum_{i=1}^n x_i ) + n \mu^2 \ ] $$ The arithmetic mean is μ=Σx_i/n, so: $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - 2 \cdot ( \frac{1}{n} \sum_{i=1}^n x_i ) \cdot ( \sum_{i=1}^n x_i ) + n \mu^2 \ ] $$ $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - 2 \cdot \frac{1}{n} ( \sum_{i=1}^n x_i )^2 + n ( \frac{1}{n} \cdot \sum_{i=1}^n x_i )^2 \ ] $$ The last term is nμ²=n(Σx_i/n)²: $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - 2 \cdot \frac{1}{n} ( \sum_{i=1}^n x_i )^2 + \frac{1}{n} \cdot \sum_{i=1}^n x_i^2 \ ] $$ $$ \sigma^2 = \frac{1}{n} \cdot \ [ \ \sum_{i=1}^n x_i^2 - \frac{1}{n} \cdot \sum_{i=1}^n x_i ^2 \ ] $$ $$ \sigma^2 = \frac{1}{n} \cdot \sum_{i=1}^n x_i^2 - \frac{1}{n} \cdot \frac{1}{n} \cdot \sum_{i=1}^n x_i ^2 $$ $$ \sigma^2 = \frac{1}{n} \cdot \sum_{i=1}^n x_i^2 - \frac{1}{n^2} \cdot \sum_{i=1}^n x_i ^2 $$ $$ \sigma^2 = ( \frac{1}{n} \cdot \sum_{i=1}^n x_i^2) - (\frac{1}{n} \cdot \sum_{i=1}^n x_i) ^2 $$ The first term is the square of the quadratic mean (μ_q)², and the second term is the square of the arithmetic mean μ². This proves the result: $$ \sigma^2 = \mu_q^2 - \mu^2 $$

• Sheppard's correction
  When data is grouped into classes, it introduces some approximation in the calculation of variance. To correct for this, Sheppard’s correction is applied: $$ \sigma^2_R = \sigma^2 - \frac{ \alpha^2 }{12} $$ Where σ² is the variance, and α is the class width.

  Note. Some level of approximation occurs with all indicators when data is grouped into classes, but it is particularly pronounced with variance because variance is based on the square of the unit of measurement of the observed phenomenon.

And so on.