Average Absolute Deviation

What is average absolute deviation?

Average absolute deviation (AAD) is a measure of variability that sums the absolute differences (or deviations) of each element in a distribution (x_i) from the average (μ). $$ S = \frac{1}{n} \cdot \sum_{i=1}^n | x_i - \mu | $$ In this formula, μ can refer to either the arithmetic mean or the median.

It is also referred to as the mean absolute deviation (MAD) for the arithmetic mean and is one of the key indicators of absolute variability.

Why is it useful?

Mean absolute deviation gives us a measure of how spread out the data is within a population or statistical distribution.

The deviations from the mean are taken in absolute terms to prevent them from canceling each other out, which would obscure information about the data’s dispersion.

Note: In the case of a frequency distribution, the following formula is used to calculate the mean absolute deviation: $$ S = \frac{ \sum |x_i - \mu| \cdot n_i}{ \sum n_i } $$

A practical example

Let’s look at this statistical distribution with n=6 elements:

$$ x = \{ 4, 2, 6, 8, 7, 3 \} $$

The arithmetic mean of this distribution is m=5

$$ \mu = \frac{4+2+6+8+7+3}{6} = \frac{30}{6} = 5 $$

Now, we can calculate the mean absolute deviation from the arithmetic mean:

$$ S = \frac{1}{n} \cdot [ |4 - \mu| + |2 - \mu | + |6 - \mu| + |8 - \mu| + |7 - \mu | + |3 - \mu | ] $$

Given that n=6 and the arithmetic mean is m=5, we have:

$$ S = \frac{1}{6} \cdot [ |4- 5| + |2 - 5 | + |6 - 5| + |8 - 5| + |7- 5 | + |3 - 5 | ] $$

$$ S = \frac{1}{6} \cdot [ |-1| + | -3 | + |1| + |3| + |2 | + | -2 | ] $$

$$ S = \frac{1}{6} \cdot [ 1 + 3 + 1 + 3 + 2 + 2 ] $$

$$ S = \frac{1}{6} \cdot 12 $$

$$ S = 2 $$

So, the mean absolute deviation is S=2.

Example 2

Now, consider this frequency distribution, where the scores represent the categories:

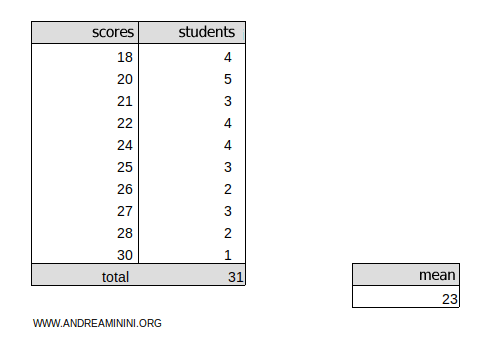
The weighted arithmetic mean is μ=23.

To calculate the mean absolute deviation, we use this formula:

$$ S = \frac{ \sum |x_i - \mu| \cdot n_i}{ \sum n_i } $$

Here, x_i represents the scores, and n_i refers to the frequency of each score.

The sum of the frequencies is Σn=31, and the mean is μ=23.

$$ S = \frac{ \sum |x_i - 23| \cdot n_i}{ 31 } $$

$$ S = \frac{ |18-23| \cdot 4 + |20-23| \cdot 5 + |21-23| \cdot 3 + |22-23| \cdot 4 + |24-23| \cdot 4 + \\ + |25-23| \cdot 3 + |26-23| \cdot 2 + |27-23| \cdot 3 + |28-23| \cdot 2 + |30-23| \cdot 1 }{ 31 } $$

$$ S = \frac{ |-5| \cdot 4 + |-3| \cdot 5 + |-2| \cdot 3 + |-1| \cdot 4 + |1| \cdot 4 + \\ + |2| \cdot 3 + |3| \cdot 2 + |4| \cdot 3 + |5| \cdot 2 + |7| \cdot 1 }{ 31 } $$

$$ S = \frac{ 5 \cdot 4 + 3 \cdot 5 + 2 \cdot 3 + 1 \cdot 4 + 1 \cdot 4 + 2 \cdot 3 + 3 \cdot 2 + 4 \cdot 3 + 5 \cdot 2 + 7 \cdot 1 }{ 31 } $$

$$ S = \frac{ 20 + 15 + 6 + 4 + 4 + 6 + 6 + 12 + 10 + 7 }{ 31 } $$

$$ S = \frac{ 90 }{ 31 } $$

$$ S = 2.9 $$

The mean absolute deviation of this distribution is S=2.9.

Notes

Here are a few observations:

• Why are deviations taken in absolute terms?
  When calculating the mean absolute deviation, we use the absolute values of deviations to avoid positive and negative deviations from canceling each other out. In particular, the arithmetic mean of the deviations without taking absolute values is always zero, which tells us nothing useful about the variability or spread of the data. For example, consider a distribution of n values x₁,x₂,...,x_n with an arithmetic mean μ. The mean of the deviations without absolute values is: $$ \frac{(x_1 - \mu)+(x_2 - \mu)+...+(x_n - \mu)}{n} $$ Applying the associative and commutative properties of addition: $$ \frac{x_1+x_2+...+x_n - \underbrace{ \mu - \mu- \mu}_{n \ times} }{n} $$ The arithmetic mean μ appears n times: $$ \frac{x_1+x_2+...+x_n - n \cdot \mu }{n} $$ Simplifying: $$ \frac{x_1+x_2+...+x_n }{n} - \frac{n \cdot \mu}{n} $$ $$ \underbrace{ \frac{x_1+x_2+...+x_n}{n} }_{ \mu } - \mu $$ Since the first term is always the arithmetic mean, $ \mu =  \frac{x_1+x_2+...+x_n }{n} $, the sum cancels out: $$ \mu - \mu = 0 $$ Therefore, the sum of the deviations from the mean is always zero. This is why the mean absolute deviation uses absolute values—to prevent the deviations from canceling each other out and to provide a useful measure of data dispersion.

  Example: Consider the distribution $$ 2, 4, 6, 8, 10 $$ The arithmetic mean of these numbers is 6. $$ \mu = \frac{2+4+6+8+10}{5} = \frac{30}{5} = 6 $$ The deviations from the mean are: $$ 2 - 6 = -4 \\ 4 - 6 = -2 \\ 6 - 6 = 0 \\ 8 - 6 = 2 \\ 10 - 6 = 4 $$ The sum of the deviations is zero: $$ (-4) + (-2) + 0 + 2 + 4 = 0 $$ In this case, the arithmetic mean of the deviations provides no information about the spread. $$ \frac{(-4) + (-2) + 0 + 2 + 4}{5} = \frac{0}{5}=0 $$ However, by using the absolute values, the sum of the deviations becomes a non-negative number: $$ |-4| + |-2| + |0| + |2| + |4| = 4+2+0+2+4= 12 $$ Therefore, the arithmetic mean of the absolute deviations is also non-negative: $$ \frac{4 + 2 + 0 + 2 + 4}{5} = 2.4 $$ This value represents the average spread of the data from the arithmetic mean.

And that’s how it works.