Finding the Minimum and Maximum of a Function of Two Variables Using Level Curves
The level curve method is a graphical technique used to identify the maximum or minimum of a function $f(x, y)$ over a set $A$, meaning within its domain.
It is an intuitive and visual approach, especially effective for simple functions and bounded domains (such as polygons).
What are level curves?
Level curves are the contours in the $(x, y)$ plane along which the function $f(x, y)$ remains constant:
$f(x, y) = \lambda$
In other words, each level curve consists of all the points in the plane where the function equals the same value $\lambda$.
How does the method work?
The method is straightforward and relies on geometric reasoning:
- Draw the domain $A$
- Plot the set $A$ in the $(x,y)$ plane. This defines the region where you will search for the function’s maximum and minimum.
- Plot the level curves of $f(x, y)$
- Draw several curves $f(x, y) = \lambda$ for different values of $\lambda$. Each curve shows where the function equals $\lambda$.
- Identify the maximum and minimum
The maximum corresponds to the highest level curve (i.e. the largest $\lambda$) that intersects or touches $A$.
The minimum corresponds to the lowest level curve (i.e. the smallest $\lambda$) that touches $A$.
When is this method useful? This method works very well for simple or symmetric functions (such as those involving squares, circles, or ellipses) and for polygonal or bounded domains. In other words, in situations where it is possible to visually understand how the function behaves. For more complex functions or irregular domains, this approach still offers valuable qualitative insights before moving on to more rigorous analytical methods.
Example
Let’s consider the following function:
$f(x, y) = x^2 + y^2$
and the domain $A$, defined as the square $-1 \leq x \leq 1$, $-1 \leq y \leq 1$.
First, we plot the square $A$ in the $(x, y)$ plane.

The level curves of this function are circles of radius $\sqrt{\lambda}$ centered at the origin.
$$ x^{2}+y^{2}=\lambda,\qquad \lambda\ge 0. $$
Solving for $y$, we obtain:
$$ y^{2}=\lambda-x^{2}\quad\Longrightarrow\quad y=\pm\sqrt{\lambda-x^{2}} $$
In order for a level curve to intersect the domain $A$, the corresponding value of $\lambda$ must be large enough for the circle to reach or touch $A$.
Next, we plot the level curves by varying $ \lambda $.
Since $ \lambda \ge 0 $, only non-negative values are admissible.

The smallest level curve that intersects $A$ is the degenerate circle of radius 0, corresponding to the single point $(0,0)$, where $f(0,0) = 0$.
Therefore, the absolute minimum of the function over this domain is $0$, attained at the point $ (x,y)=(0,0) $.
The largest level curve that still touches the domain is the circle passing through the vertices of the square.
$$f(1,1) = 1^2 + 1^2 = 2$$
Thus, the absolute maximum of the function over the domain is $2$, attained at the points $(1,1)$, $(-1,1)$, $ (1,-1) $, and $ (-1,-1) $.
With a simple sketch, we have identified both the minimum and maximum values of the function.

Example 2
Consider the function
$$ f(x,y) = x - 2y $$
subject to the constraint
$$ x^2 + y^2 \le 3 $$
Our goal is to determine the maximum and minimum values of the function within this constraint, using the method of level curves.
We begin by plotting the constraint, which in this case is the circle $ x^2 + y^2 \le 3 $.
The function takes various values along the z-axis, which we denote by $ \lambda $:
$$ f(x,y) = x - 2y = \lambda $$
We can express $ y $ in terms of $ x $ and $ \lambda $:
$$ x - \lambda = 2y $$
$$ y = \frac{x - \lambda}{2} $$
Now we sketch the level curves for different values of $ \lambda $.
Level curves corresponding to larger values of $ \lambda $ lie lower on the plane, while those corresponding to smaller values lie higher up.
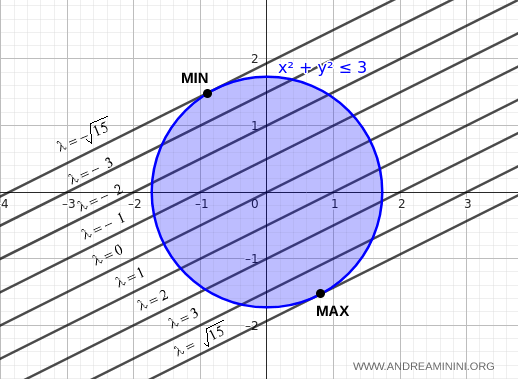
The maximum value of $ f(x,y) $ is achieved where a level curve is tangent to the lower edge of the constraint circle.
Similarly, the minimum value is attained where a level curve is tangent to the upper edge of the circle.
What are the corresponding $ \lambda $ values for the maximum and minimum?
We have the equation of the level curves:
$$ y = \frac{x - \lambda}{2} $$
Substituting this into the equation of the circle’s boundary gives:
$$ x^2 + \left( \frac{x - \lambda}{2} \right)^2 = 3 $$
$$ x^2 + \frac{(x - \lambda)^2}{4} = 3 $$
Multiplying through by 4 to eliminate denominators:
$$ 4x^2 + (x - \lambda)^2 = 12 $$
Expanding the square:
$$ 4x^2 + x^2 - 2x\lambda + \lambda^2 = 12 $$
$$ 5x^2 - 2x\lambda + \lambda^2 = 12 $$
We now have a quadratic equation in $ x $.
To find when the level curve is tangent to the circle, we require the equation to have exactly one solution - that is, the discriminant must be zero:
$$ \Delta = [-2\lambda]^2 - 4 \cdot 5 \cdot (\lambda^2 - 12) $$
$$ \Delta = 4\lambda^2 - 20(\lambda^2 - 12) $$
$$ \Delta = 4\lambda^2 - 20\lambda^2 + 240 $$
$$ \Delta = -16\lambda^2 + 240 $$
Setting $ \Delta = 0 $:
$$ -16\lambda^2 + 240 = 0 $$
$$ 16\lambda^2 = 240 $$
$$ \lambda^2 = \frac{240}{16} $$
$$ \lambda^2 = 15 $$
$$ \lambda = \pm \sqrt{15} $$
Thus, the maximum and minimum values of $ f(x,y) $ under the given constraint are:
$$ \lambda_{max} = \sqrt{15} \approx 3.873 $$
$$ \lambda_{min} = -\sqrt{15} \approx -3.873 $$
And so on.
