First Principle of Equation Equivalence

According to the first principle of equation equivalence, if we add or subtract the same value or expression $k$ to both sides of an equation, the resulting equation is equivalent to the original one. $$ a = b \ \ \Leftrightarrow a+k = b+k $$

In other words, if we start with an equation like

$$ a = b $$

we can add the same value or expression to both sides, and the equality remains valid:

$$ a + k = b + k $$

Similarly, we obtain an equivalent equation if we subtract the same value or expression from both sides:

$$ a - k = b - k $$

Note. Two or more equations are considered equivalent if they share the exact same set of solutions.

Why is the first principle of equivalence important?

This principle is extremely useful because it allows us to simplify an equation step by step, transforming it into a form that’s easier to solve.

A Practical Example

Let’s look at the equation:

$$ 8x + 5 = 13x - 7 $$

We can apply the first principle of equation equivalence by subtracting $8x$ from both sides:

$$ 8x + 5 \color{red}{-8x} = 13x - 7 \color{red}{-8x} $$

This eliminates the $8x$ term from the left-hand side and effectively transfers it to the right-hand side with the opposite sign.

After simplifying, we have:

$$ 5 = 13x - 7 - 8x $$

Now, we can combine the like terms $13x - 8x$:

$$ 5 = 5x - 7 $$

Next, let’s apply the first principle once more by adding $7$ to both sides:

$$ 5 \color{red}{+7} = 5x - 7 \color{red}{+7} $$

This moves the $-7$ term to the left-hand side, changing its sign and allowing us to add it to $5$:

$$ 12 = 5x $$

Through this process, we’ve simplified the original equation and made it much easier to solve.

 

Note. The first principle of equivalence works much like a balance scale in physics. If a scale is perfectly balanced and you add or remove the same weight from both pans, the balance remains unchanged. The same idea applies to an equation: as long as you perform the same operation on both sides, the equality holds true.

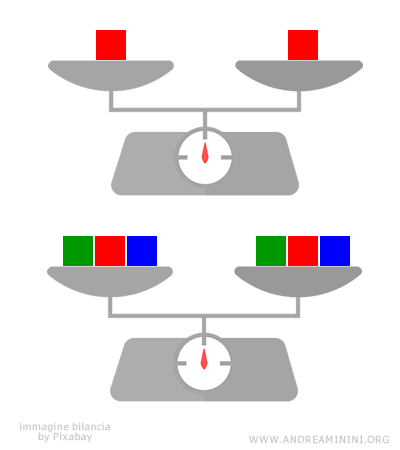
And so on.