Linear Combination of Two Equations

A linear combination of two or more equations $$ ax + by + c = 0 $$$$ a'x + b'y + c' = 0 $$ is obtained by adding or subtracting the given equations, possibly after multiplying them by constant coefficients (α, β, ...): $$ \alpha(ax + by + c) + \beta(a'x + b'y + c') = 0 $$

This method is particularly useful because it is widely applied in solving systems of linear equations through the elimination or reduction method.

A Practical Example

Consider the following pair of linear equations:

$$ 3x + 4y -5 = 0 $$

$$ 2x - 3y +2 = 0 $$

These represent two lines that intersect at a single point.

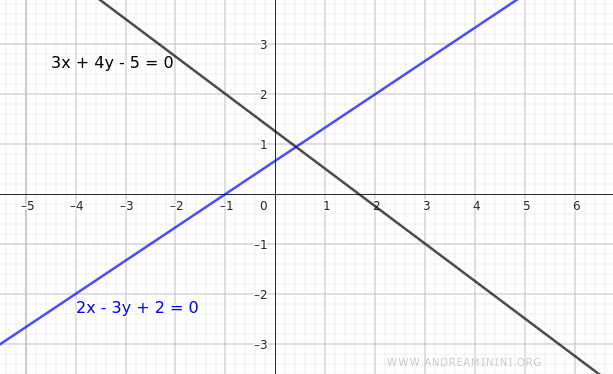
Let us choose two scalar parameters, α and β, which we will use as coefficients to form a linear combination of the two equations.

In general, the coefficients α and β can be any real numbers - integers, fractions, positive or negative.

For instance, let α = 2 and β = 3.

$$ \alpha = 2 $$

$$ \beta = 3 $$

The linear combination of these two equations can be written as:

$$ \alpha(ax + by + c) + \beta(a'x + b'y + c') = 0 $$

$$ 2 \cdot (3x + 4y -5) + 3 \cdot(2x -3y + 2) = 0 $$

Expanding and simplifying the terms gives:

$$ 6x + 8y -10 + 6x -9y + 6 = 0 $$

Combining like terms yields:

$$ (6x + 6x) + (8y - 9y) -10 + 6 = 0 $$

$$ 12x - y - 4 = 0 $$

The final result is another linear equation.

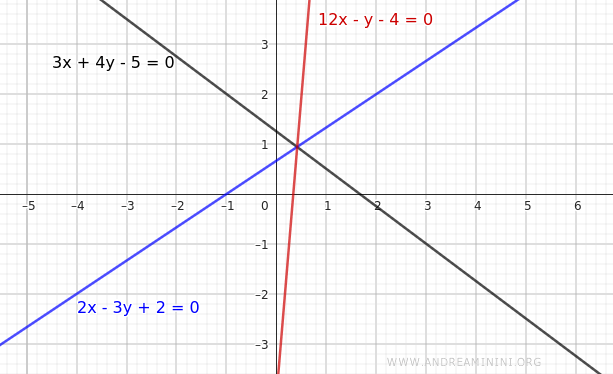
Note. The new linear equation obtained through this combination (in red) passes through the same intersection point as the two original lines (in blue and black).

Properties of Linear Combinations of Equations

Linear combinations of equations possess several important algebraic properties, particularly within the context of linear systems.

The most significant ones include:

• Closure
  The sum or linear combination of two linear equations is itself a linear equation. This means that the set of all linear equations is closed under addition and scalar multiplication.

  Example. Consider two first-degree equations: $$ 3x + 4y -5 = 0 $$$$ 2x - 3y +2 = 0 $$ Their linear combination with coefficients α=2 and β=3 yields another linear equation: $$ 2 \cdot (3x + 4y -5) + 3 \cdot(2x -3y + 2) = 0 $$ $$ 12x - y - 4 = 0 $$

• Commutativity
  The order in which equations are added does not affect the result. If \( E_1 \) and \( E_2 \) are two linear equations, then: $$ \alpha E_1 + \beta E_2 = \beta E_2 + \alpha E_1 $$

  Example. Consider the equations $$ 3x + 4y -5 = 0 $$$$ 2x - 3y +2 = 0 $$ Their linear combination with α=2 and β=3 is: $$ 2 \cdot (3x + 4y -5) + 3 \cdot(2x -3y + 2) = 0 $$ $$ 12x - y - 4 = 0 $$ Reversing the order of addition gives the same result: $$ 3 \cdot(2x -3y + 2) + 2 \cdot (3x + 4y -5) = 0 $$ $$ 12x - y - 4 = 0 $$

• Associativity
  Addition of linear equations is associative. For three linear equations \( E_1, E_2, \) and \( E_3 \), we have: $$ (\alpha E_1 + \beta E_2) + \gamma E_3 = \alpha E_1 + (\beta E_2 + \gamma E_3) $$
• Neutral Element (Zero Equation)
  The neutral element for addition is the zero equation \( 0x + 0y = 0 \), which leaves any linear equation unchanged when added to it.

  Example. Consider the equation $$ 3x + 4y -5 = 0 $$ Adding the zero equation produces no change: $$ (3x + 4y -5) + (0x+0y+0) = 0 $$ $$ 3x + 4y -5 = 0 $$

• Opposite Element
  For every linear equation \( ax + by = c \), there exists an opposite equation \( -ax - by = -c \), such that their sum is the zero equation.

  Example. Consider $$ 3x + 4y -5 = 0 $$ The opposite equation is obtained by multiplying by -1, giving \( -(3x+4y-5)=0 \), or equivalently \( -3x - 4y + 5 = 0 \). $$ (3x + 4y -5) + (-3x - 4y + 5) = 0 $$ $$ 0 = 0 $$

• Scalar Multiplication
  Multiplying any linear equation by a nonzero scalar produces another equation that is algebraically equivalent to the original. For example, multiplying both sides of \( ax + by = c \) by \( k \neq 0 \) gives \( kax + kby = kc \), which has the same set of solutions as the original equation.
  

  Example. Consider $$ 3x + 2y -6 = 0 $$ Multiply the equation by 2: $$ 2 \cdot (3x+2y-6)= 2 \cdot 0 $$ The resulting equation is equivalent, since it has the same solution set (e.g., x=2, y=0 or x=0, y=3, etc.): $$ 6x + 4y -12 = 0 $$  Geometrically, both equations represent the same line in the coordinate plane - that is, they are coincident.
  

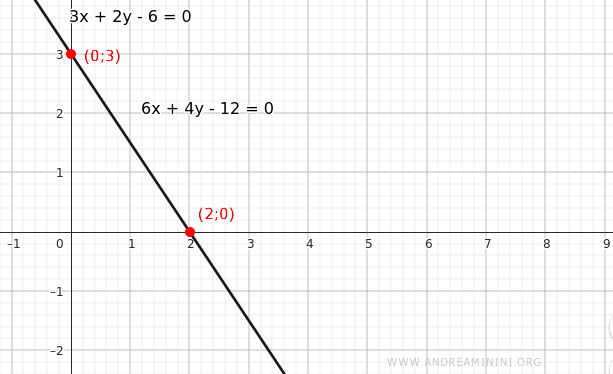
• Linear Independence and Dependence
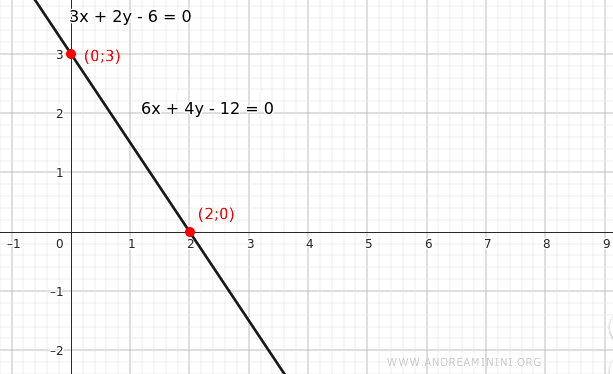
  A set of equations is linearly independent if none of them can be expressed as a linear combination of the others. If one equation can be expressed in terms of the others, the set is linearly dependent. This concept is fundamental in determining whether a system of equations admits a unique solution.
  

  Example. The equations $ 3x + 2y - 6 = 0 $ and $ 6x + 4y - 12 = 0 $ are linearly dependent, because the second is simply twice the first. Conversely, dividing the second by 2 gives the first. Hence, the two equations coincide and describe the same line in the plane. Saying that two equations are linearly dependent therefore means that they represent exactly the same geometric locus.
  

These properties are fundamental for algebraic manipulation within systems of equations and are extensively applied across linear algebra, including in the analysis of systems of equations, vector theory, and the study of vector spaces.

Remarks

Additional notes and observations:

• Linear Combination of Higher-Degree Equations
  When combining equations of degree higher than one, even with different degrees, the resulting polynomial will have a degree equal to the highest among the originals, unless specific cancellations occur.

  Example. Combining a quadratic and a cubic polynomial generally produces a cubic equation, though it may result in a lower degree depending on the chosen coefficients. For example, consider these two quadratic equations: $$ 3x^2 + 2x - 1 = 0 $$ $$ 3x^2 + x + 2 = 0 $$ and choose coefficients α = 1 and β = 1. Their linear combination is another quadratic: $$ 1 \cdot (3x^2 + 2x - 1) + 1 \cdot (3x^2 + x + 2) = 0 $$ $$ 6x^2 + 3x + 1 = 0 $$ If instead we choose α = 1 and β = -1, the quadratic terms cancel, resulting in a first-degree equation: $$ 1 \cdot (3x^2 + 2x - 1) - 1 \cdot (3x^2 + x + 2) = 0 $$ $$ x - 3 = 0 $$

• If (x, y) is a solution to both linear equations $ ax + by + c = 0 $ and $ a'x + b'y + c' = 0 $, then it is also a solution to any linear combination of them: $$ \alpha \cdot (ax + by + c) + \beta \cdot (a'x + b'y + c') = 0 $$

  Proof. This follows because the ordered pair (x, y) satisfies both equations, making each expression equal to zero. Therefore, any linear combination will also be zero. $$ \alpha \cdot \underbrace{(ax + by + c)}_{=0} + \beta \cdot \underbrace{(a'x + b'y + c')}_{=0} = 0 $$ $$ \alpha \cdot 0 + \beta \cdot 0 = 0 $$

And so on.