Parametric System of Equations

A system of equations is called a parametric system when at least one equation contains one or more parameters.

An equation involves parameters when, alongside its unknowns, it includes certain constants treated as adjustable values.

These parameters are unspecified constants that may take different numerical values.

Nota. Although no strict notation rule exists, parameters are commonly written using the first lowercase letters of the alphabet such as a, b, c, k. Unknown variables are usually denoted by the last lowercase letters x, y, z.

A practical example

Consider the following parametric system:

$$ \begin{cases} x+2y=4 \\ \\ ax+y=2 \end{cases} $$

We solve the system by substitution:

$$ \begin{cases} y=\frac{4-x}{2} \\ \\ y=2-ax \end{cases} $$

Equating the two expressions for y gives:

$$ \frac{4-x}{2} = 2-ax $$

Multiply both sides by 2:

$$ 4-x = 2 \cdot (2-ax) $$

Expand the right side:

$$ 4-x = 4-2ax $$

Group the x terms on one side:

$$ -x - 2ax = 4 $$

Factor out x:

$$ x \cdot (2a-1) = 4 $$

The factor $2a - 1$ becomes zero when:

$$ a = \frac{1}{2} $$

In this case the equation cannot be satisfied, because multiplying any value of x by zero can never produce 4.

Hence, when $a = 1/2$ the system has no solutions and is therefore inconsistent.

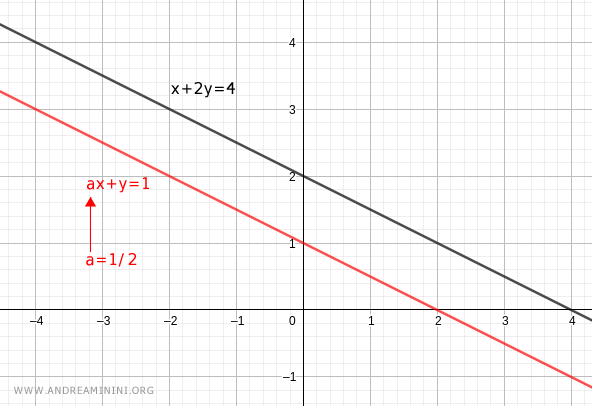
the system has no solution when a equals one half

Nota. When $a = 1/2$ the two lines defined by the equations have the same slope and are parallel. Parallel lines never intersect, which means the system has no solution.

For any value $a \ne 1/2$ the system admits exactly one solution, so it is consistent and has a unique solution.

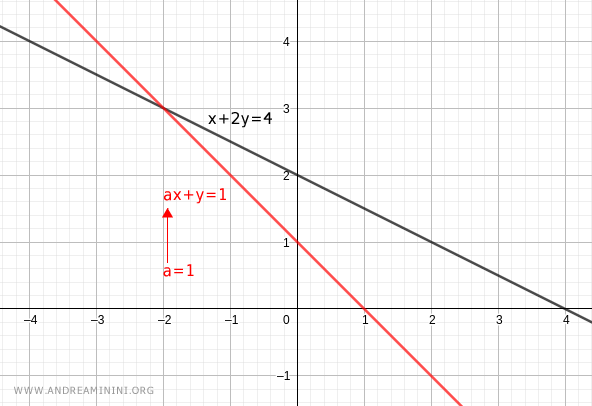
the system has a unique solution when the parameter a is not equal to one half

And so on.