Parametric Equations

A parametric equation is an algebraic expression that includes one or more letters called parameters, distinct from the unknown variable. These parameters determine the specific conditions under which the equation is satisfied.

When analyzing a parametric equation, we must take into account all the possible values that the parameters can assume.

If a particular condition is imposed by the problem, our goal is to determine the parameter values that satisfy that condition.

A practical example

Consider the following quadratic parametric equation:

$$ x^2 - 2kx + 5k - 6 = 0 $$

Here, k is the parameter and x is the variable.

We are asked to find the value of k for which the equation has two equal real roots (this is the condition to be met).

Note. In this case, the condition is explicitly given. Therefore, we must identify the parameter values that satisfy it.

This condition requires that the discriminant be equal to zero, that is, Δ = 0.

$$ \Delta = b^2 - 4ac = 0 $$

The coefficients of the equation are a = 1, b = -2k, and c = 5k - 6.

$$ b^2 - 4ac = 0 $$

$$ (-2k)^2 - 4 \cdot (1) \cdot (5k - 6) = 0 $$

$$ 4k^2 - 20k + 24 = 0 $$

This is a quadratic equation in the variable k.

Let’s solve it to find the values of k that satisfy the equation:

$$ k = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

In this case, the coefficients are a = 4, b = -20, and c = 24.

$$ k = \frac{-(-20) \pm \sqrt{(-20)^2 - 4 \cdot 4 \cdot 24}}{2 \cdot 4} $$

$$ k = \frac{20 \pm \sqrt{400 - 384}}{8} $$

$$ k = \frac{20 \pm \sqrt{16}}{8} $$

$$ k = \frac{20 \pm 4}{8} $$

$$ k = \begin{cases} \frac{20 - 4}{8} = \frac{16}{8} = 2 \\ \\ \frac{20 + 4}{8} = \frac{24}{8} = 3 \end{cases} $$

Therefore, when k = 2 or k = 3, the discriminant Δ = 0, and the original equation x² - 2kx + 5k - 6 = 0 has two coincident real roots.

Example 2

Let’s now consider the same quadratic equation as in the previous example, but under a different condition:

$$ x^2 - 2kx + 5k - 6 = 0 $$

This time, we must determine the values of k for which the equation has no real roots.

A quadratic equation has no real roots when the discriminant is negative, that is, Δ < 0.

$$ \Delta = b^2 - 4ac < 0 $$

The coefficients are a = 1, b = -2k, and c = 5k - 6.

$$ b^2 - 4ac < 0 $$

$$ (-2k)^2 - 4 \cdot (1) \cdot (5k - 6) < 0 $$

$$ 4k^2 - 20k + 24 < 0 $$

To solve this inequality, we first find the roots of the corresponding equation:

$$ 4k^2 - 20k + 24 = 0 $$

This is again a quadratic equation in k.

We already know its roots, k = 2 and k = 3, from the previous calculation:

$$ k = \begin{cases} \frac{20 - 4}{8} = \frac{16}{8} = 2 \\ \\ \frac{20 + 4}{8} = \frac{24}{8} = 3 \end{cases} $$

The leading coefficient a is positive (a > 0), which means the parabola opens upward.

Therefore, the quadratic expression 4k² - 20k + 24 takes negative values when k lies within the interval (2, 3).

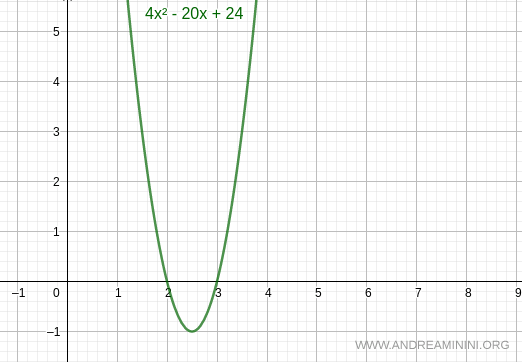
Hence, for k in the interval (2, 3), the discriminant Δ < 0, and the original equation x² - 2kx + 5k - 6 = 0 has no real roots.

Note. For completeness, we can also observe that in the external intervals (-∞, 2) ∪ (3, ∞), the discriminant Δ > 0, and the original equation x² - 2kx + 5k - 6 = 0 has two distinct real roots.

And so on.