Systems of Inequalities
A system of inequalities consists of two or more inequalities involving the same variable x. $$ \begin{cases} A(x) > B(x) \\ C(x) < D(x) \\ \vdots \\ W(x) \ge z(x) \end{cases} $$ The solution set is the collection of all real values of x that satisfy each inequality simultaneously.
Consider a first example.
$$ \begin{cases} 2x + 1 < 3 \\ \\ 4x + 3 > 5 \end{cases} $$
To solve a system of inequalities, we identify all real numbers that make every inequality true at the same time.
The first step is to solve each inequality separately.
$$ \begin{cases} 2x + 1 - 1 < 3 - 1 \\ \\ 4x + 3 - 3 > 5 - 3 \end{cases} $$
$$ \begin{cases} 2x < 2 \\ \\ 4x > 2 \end{cases} $$
$$ \begin{cases} x < 1 \\ \\ x > \frac{1}{2} \end{cases} $$
Once each inequality has been solved, we look for the interval where their solution sets overlap.
$$ \frac{1}{2} < x < 1 $$
This interval is the common solution set, that is the solution to the system.
Note. When a system includes several inequalities, representing the solution sets on a number line often provides a clear and efficient way to locate their intersection.
How to Solve a System of Inequalities
The general procedure is straightforward:
- Determine the solution set of each inequality, $$ S_1 \ , \ S_2 \ , \dots \ , \ S_n $$
- The solution to the system is the intersection of these sets, $$ S = S_1 \cap S_2 \cap \dots \cap S_n $$
Note. In practice, the solution sets are plotted on an oriented number line, known as the solution diagram. The intersection of these intervals identifies the common solution set.
If no real number satisfies all inequalities together, the system is inconsistent.
A Worked Example
Example 1
Consider the system:
$$ \begin{cases} 4x - 8 \ge 0 \\ \frac{3x - 12}{x + 1} > 0 \\ 2x - 4 < 6 \end{cases} $$
We begin constructing the solution diagram.
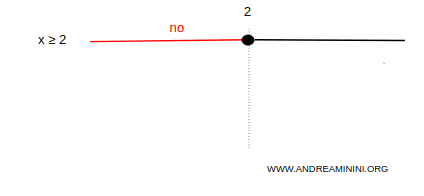
The first inequality, 4x - 8 ≥ 0, is satisfied when x ≥ 2.
$$ \begin{cases} x \ge \frac{8}{4} \\ \frac{3x - 12}{x + 1} > 0 \\ 2x - 4 < 6 \end{cases} $$
$$ \begin{cases} x \ge 2 \\ \frac{3x - 12}{x + 1} > 0 \\ 2x - 4 < 6 \end{cases} $$
Add the condition x ≥ 2 to the diagram.
The second inequality, (3x - 12)/(x + 1) > 0, is undefined at x = -1. To solve it, we examine the signs of the numerator and denominator.
- The numerator 3x - 12 is positive for x > 4.
- The denominator x + 1 is positive for x > -1.
Using sign analysis for rational inequalities, we determine where the expression is positive.
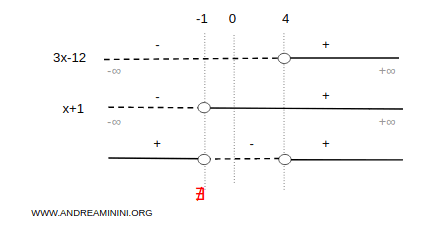
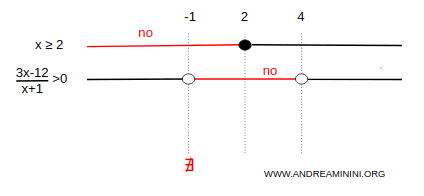
The inequality holds on the intervals (-∞, -1) U (4, ∞).
Add these intervals to the diagram.
The third inequality, 2x - 4 < 6, simplifies to x < 5.
$$ \begin{cases} x \ge 4 \\ \frac{3x - 12}{x + 1} > 0 \\ x < \frac{6 + 4}{2} \end{cases} $$
$$ \begin{cases} x \ge 4 \\ \frac{3x - 12}{x + 1} > 0 \\ x < 5 \end{cases} $$
Add the condition x < 5 to the diagram.
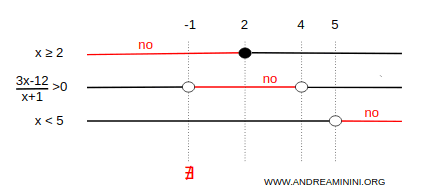
We can now determine the solution set of the system.
The three inequalities are simultaneously satisfied on the interval (4, 5).
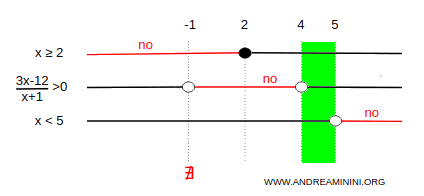
The solution set is therefore:
$$ 4 < x < 5 $$
Example 2
Consider the system:
$$ \begin{cases} x - 4 < 0 \\ 2 - x > 0 \\ x + 3 > 0 \end{cases} $$
Applying the principles of equivalence for inequalities, we solve each inequality individually.
$$ \begin{cases} x - 4 + 4 < 0 + 4 \\ 2 - x - 2 > 0 - 2 \\ x + 3 - 3 > 0 - 3 \end{cases} $$
$$ \begin{cases} x < 4 \\ -x > -2 \\ x > -3 \end{cases} $$
Multiplying both sides of the second inequality by -1 reverses the inequality sign, as required by the theory.
$$ \begin{cases} x < 4 \\ -x \cdot (-1) > -2 \cdot (-1) \\ x > -3 \end{cases} $$
$$ \begin{cases} x < 4 \\ x < 2 \\ x > -3 \end{cases} $$
We now have the complete set of solutions for the three inequalities.
Plotting them on a number line allows us to identify the intersection at a glance.
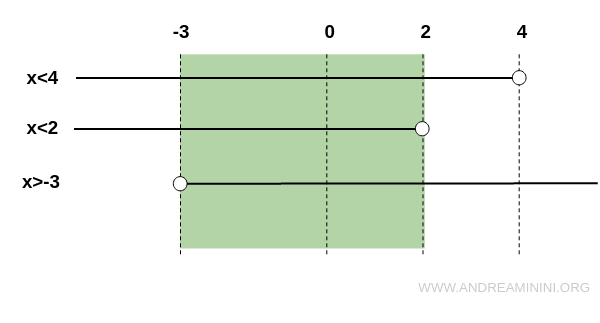
The common solution set is:
$$ -3 < x < 2 $$
This is the solution to the system.
