Parametric inequalities
A parametric inequality is an inequality in which at least one coefficient is represented by a parameter, meaning a letter whose value is not fixed and may vary over the real numbers.
Each parameter can take any real value, and the task is to determine how the solution set of the inequality depends on these choices.
For example:
$$ kx + 4 < 8 $$
In this expression, k is a parameter and x is the unknown variable.
Parameters versus variables. A parameter is a constant chosen externally, whose value may differ from one instance of the problem to another. The unknown variable is the quantity to be solved for within the inequality. Unless otherwise specified, x is treated as the unknown.
A parametric inequality may involve multiple parameters and possibly more than one variable.
Such inequalities may be either polynomial (whole) or rational (fractional), depending on whether division by expressions in the variable occurs.
How to analyze a parametric inequality
To determine the solution set, we carry out a case-by-case analysis based on the possible values of the parameters.
The main steps are:
1] For rational inequalities, begin by identifying the domain of definition, excluding values that make the denominator zero.
2] Rewrite the inequality in a standard linear form such as
$$ Ax < B $$
or
$$ Ax > B $$
where A may depend on the parameters and B denotes the constant term.
3] Perform a case analysis based on the sign of A:
- Case A > 0
- Case A = 0
- Case A < 0
4] For each case, determine the admissible solutions, meaning the values of the variable that satisfy both the inequality and, when applicable, the domain of definition.
Note. In rational inequalities, a solution is admissible only if it lies within the domain. In polynomial inequalities, all algebraic solutions are admissible.
A worked example
Consider the polynomial parametric inequality
$$ 3kx - 7k > -2 + 4kx $$
with k as the parameter and x as the unknown variable.
We rewrite the inequality in the form Ax > B.
Apply the standard equivalence rules for inequalities to collect all x - terms on the left.
Subtract 4kx from both sides:
$$ 3kx - 7k - 4kx > -2 + 4kx - 4kx $$
$$ -kx - 7k > -2 $$
Add 7k to both sides:
$$ -kx - 7k + 7k > -2 + 7k $$
$$ -kx > 7k - 2 $$
Multiply both sides by -1, reversing the inequality sign:
$$ -kx\cdot(-1) < (7k - 2)\cdot(-1) $$
$$ kx < 2 - 7k $$
The inequality is now in the standard form Ax < B, ready for case analysis.
Case analysis
We consider the possible values of k.
- Case k = 0
$$ kx < 2 - 7k $$ $$ 0\cdot x < 2 $$ $$ 0 < 2 $$ The inequality is always true, hence every real value of x is a solution. - Case k > 0
$$ kx < 2 - 7k $$ $$ \frac{kx}{k} < \frac{2 - 7k}{k} $$ Because k is positive, the inequality direction is preserved:
$$ x < \frac{2 - 7k}{k} $$ - Case k < 0
$$ kx < 2 - 7k $$ Dividing by k reverses the inequality:
$$ \frac{kx}{k} > \frac{2 - 7k}{k} $$ $$ x > \frac{2 - 7k}{k} $$
How to analyze a rational parametric inequality
For rational inequalities, a similar approach is used, but additional attention must be given to the sign of the denominator.
Main steps:
1] Rewrite the inequality in the form N/D > 0 or N/D < 0, where N and D are the numerator and denominator.
2] Combine terms to obtain a single rational expression.
3] Identify the domain of definition, excluding roots of the denominator.
4] Perform a case analysis with respect to the parameter:
- Case k > 0
- Case k = 0
- Case k < 0
Within each case, determine when the numerator and denominator are positive or negative. This sign analysis allows us to locate the intervals where the rational expression satisfies the inequality.
Only admissible solutions are retained, that is, those consistent with both the inequality and the domain.
Note. A solution is admissible only if it satisfies the inequality and remains within the domain established by the denominator.
A worked example
Consider the rational parametric inequality:
$$ \frac{1}{k} > \frac{1}{x} $$
with k as parameter.
Rewrite the inequality as a single rational expression:
$$ \frac{1}{k} - \frac{1}{x} > 0 $$
Bring the terms to a common denominator:
$$ \frac{x - k}{kx} > 0 $$
The expression is undefined at x = 0, so the domain of definition is
$$ D.D.\ x \neq 0 $$
Case analysis
We examine the possible values of k.
- Case k = 0
The expression is undefined because the denominator kx is zero. - Case k > 0
Sign analysis of numerator and denominator:
$$ x - k > 0 \Longrightarrow x > k $$ $$ kx > 0 \Longrightarrow x > 0 $$ The sign chart is shown below:
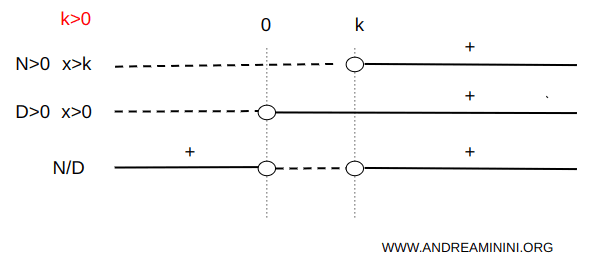
The inequality holds for x < 0 and x > k:
$$ \forall\ x < 0 \ \text{and}\ x > k $$ - Case k < 0
Sign analysis for negative k:
$$ x - k > 0 \Longrightarrow x > k $$ $$ kx > 0 \Longrightarrow x < 0 $$Note. Since k is negative, dividing by k reverses the inequality direction.
The corresponding sign chart is:
$$ kx > 0 $$ $$ \frac{kx}{k} < \frac{0}{k} $$ $$ x < 0 $$
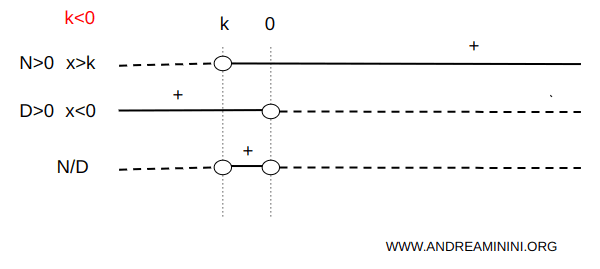
The inequality holds when x > k and x < 0:
$$ \forall\ x > k \ \text{and}\ x < 0 $$ which corresponds to the interval k < x < 0.
This method extends naturally to more intricate parametric inequalities and provides a systematic framework for understanding how the solution set varies with the parameter.
