Logarithmic inequalities
A logarithmic inequality is an inequality in which the unknown appears as the argument of at least one logarithm. $$ \log_b P(x) > \log_b Q(x) $$
How to solve a logarithmic inequality
Logarithmic inequalities can be solved using either an algebraic approach or a graphical approach.
1) The algebraic method
This method consists in setting up and solving a system that includes
- the existence conditions of the logarithms
- the inequality obtained by comparing their arguments
- Warning. When forming the inequality between the arguments, particular care must be taken with the base of the logarithms.
- If the base is greater than one, b>1, the inequality between the arguments has the same direction as the logarithmic inequality $$ \log_b P(x) > \log_b Q(x) \Rightarrow P(x) > Q(x) $$
- If the base lies between zero and one, 0< b<1, the inequality between the arguments has the opposite direction to the logarithmic inequality $$ \log_b P(x) > \log_b Q(x) \Rightarrow P(x) < Q(x) $$
2) The graphical method
A Cartesian coordinate system is used.
- the graphs of both sides of the inequality are plotted
- the intervals over which the inequality holds are determined
Note. The graphical method is especially useful when the algebraic method is impractical or excessively cumbersome. This typically happens when the unknown appears in additional algebraic expressions beyond the argument of the logarithm. In such cases, a graphical analysis is often the most effective approach.
A worked example
Consider the following logarithmic inequality.
$$ \log_{\frac{1}{2}} x > 2 $$
The existence condition (E.C.) of the logarithm is x>0.
To proceed, the constant 2 must be expressed as a logarithm with base 1/2.
Since 2 = log1/2 1/4
$$ \log_{\frac{1}{2}} x > \log_{\frac{1}{2}} \frac{1}{4} $$
Explanation. To determine the argument of a logarithm with base 1/2 that equals 2, it is sufficient to raise the base to the second power. $$ b^2 = ( \frac{1}{2} )^2 = \frac{1}{4} $$
The two logarithms now have the same base.
The invariance property of equations is applied by raising both sides to a power with base 1/2.
Since the base lies between 0 and 1, the direction of the inequality reverses from > to <.
$$ ( \frac{1}{2} )^{ \log_{\frac{1}{2}} x } < ( \frac{1}{2} )^{ \log_{\frac{1}{2}} \frac{1}{4} } $$
The exponential and logarithmic expressions simplify.
This leads to the inequality between the arguments.
$$ x < \frac{1}{4} $$
At this point, a system combining the existence condition and the inequality between the arguments is set up.
$$ \begin{cases} x>0 \\ \\ x < \frac{1}{4} \end{cases} $$
The solution set of the system is
$$ 0 < x < \frac{1}{4} $$
This interval is also the solution set of the logarithmic inequality.
Therefore, the logarithmic inequality is satisfied for all values of x between zero and one quarter.
Example 2 (graphical method)
The same inequality is now solved using the graphical method.
$$ \log_{\frac{1}{2}} x > 2 $$
The left-hand side of the inequality corresponds to the logarithmic function of x with base 1/2.
The function y=log1/2 x is plotted on a Cartesian plane.
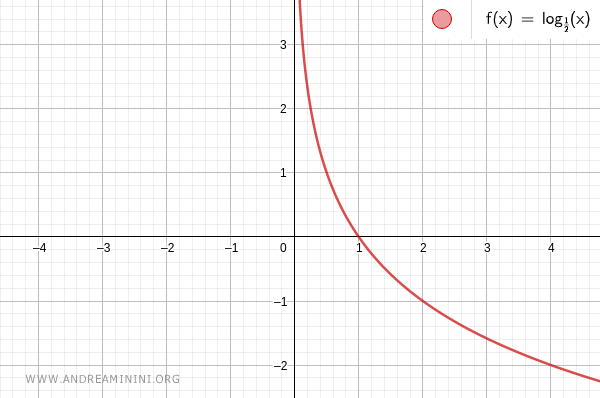
The right-hand side of the inequality is the constant value 2.
The horizontal line y=2 is added to the same graph.
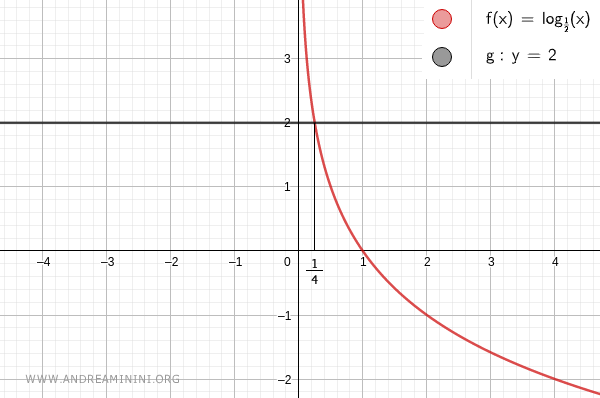
The point of intersection of the two graphs is x0=1/4.
Consequently, the inequality is satisfied on the interval (0,1/4).
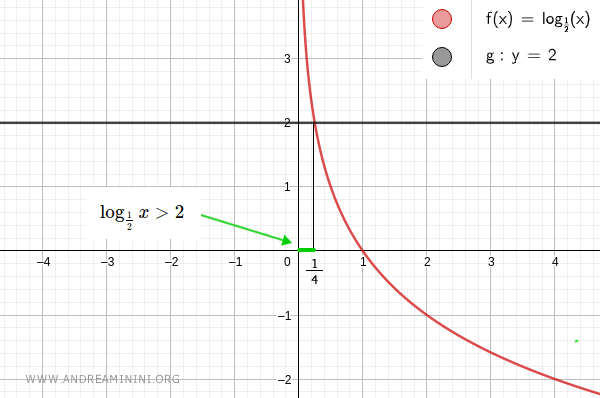
This result agrees with the one previously obtained using the algebraic method.
And so on.
