Biquadratic Inequalities

A biquadratic inequality is a fourth degree inequality of the form $$ ax^4 \pm bx^2 \pm c \gt 0 $$ or $$ ax^4 \pm bx^2 \pm c \lt 0 $$ where the coefficient a is nonzero a<>0.

To tackle a biquadratic inequality, we introduce an auxiliary variable that streamlines the expression.

$$ t = x^2 $$

This substitution converts the original inequality into a standard quadratic inequality, which is far more straightforward to analyze.

$$ at^2 \pm bt + c \gt 0 $$

Once the quadratic inequality is solved, we revert to the original variable by replacing t with x.

A worked example

Consider the inequality

$$ 2x^4 - 7x^2 - 4 \lt 0 $$

This is a biquadratic inequality with a≠0.

We begin by introducing the auxiliary variable t.

$$ t = x^2 $$

Substituting t for x² gives the equivalent quadratic inequality

$$ 2t^2 - 7t - 4 \lt 0 $$

To solve it, we first examine the associated quadratic equation.

$$ 2t^2 - 7t - 4 = 0 $$

The graph of this equation is an upward opening parabola.

The discriminant is positive Δ = (-7)² - 4⋅2⋅(-4) = 81, which confirms that the equation 2t² - 7t - 4 = 0 has two distinct real solutions.

$$ t = \frac{-(-7) \pm \sqrt{(-7)^2 - 4 \cdot 2 \cdot (-4)}}{2 \cdot 2} $$

$$ t = \frac{7 \pm \sqrt{49 + 32}}{4} $$

$$ t = \frac{7 \pm \sqrt{81}}{4} $$

$$ t = \frac{7 \pm 9}{4} = \begin{cases} t_1 = \frac{7 - 9}{4} = -\frac{1}{2} \\ \\ t_2 = \frac{7 + 9}{4} = 4 \end{cases} $$

The two real roots are t₁ = -1/2 and t₂ = 4, ordered so that t₁ < t₂.

Since the parabola opens upward, the quadratic expression is negative within the open interval (t₁, t₂) = (-1/2, 4) and positive outside it.

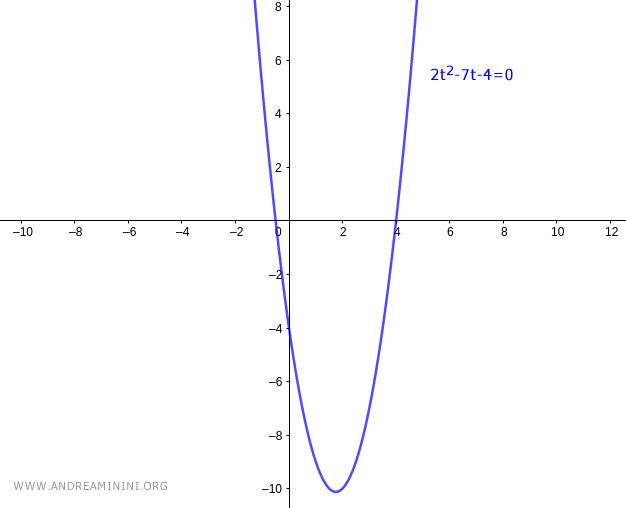
It follows that the inequality 2t² - 7t - 4 < 0 is satisfied for t ∈ (-1/2, 4).

$$ -\frac{1}{2} < t < 4 $$

We now return to the original variable, recalling that t = x².

$$ -\frac{1}{2} < x^2 < 4 $$

Note. Once we substitute back, it becomes immediately evident that the lower bound cannot hold, because x² is never negative over the set of real numbers. For this reason, we can ignore the inequality x² > -1/2 and focus solely on x² < 4.

We now extract the square roots.

$$ \sqrt{-\frac{1}{2}} < \sqrt{x^2} < \sqrt{4} $$

The left side does not yield real values, so it contributes no constraints.

Thus x must lie within the interval x ∈ (-2, 2).

$$ x < \pm 2 $$

or equivalently

$$ -2 < x < 2 $$

This is the complete solution to the original biquadratic inequality 2x⁴ - 7x² - 4 < 0.

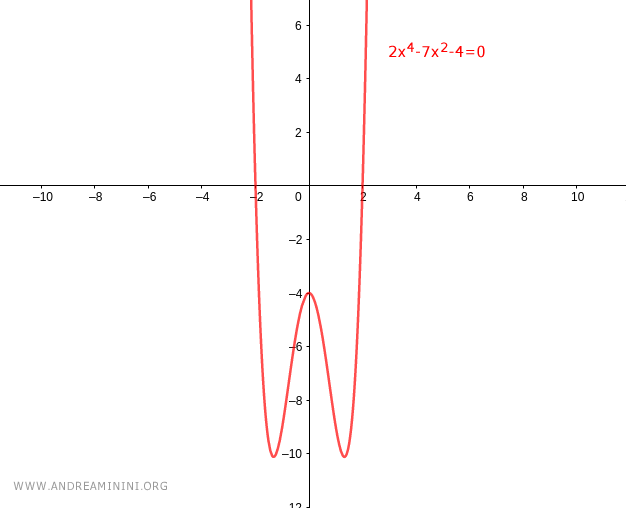
And the same method can be applied systematically to any biquadratic inequality.