Properties of Numerical Inequalities
Numerical inequalities follow several key properties.
These properties are extremely useful because they let us simplify inequalities, making it easier to solve mathematical problems.
Additive Property
If I add or subtract the same number from both sides of an inequality, the inequality remains true and keeps the same direction.
$$ a < b \Leftrightarrow a + c < b + c $$
Example. Let’s take the inequality $$ 4 > 2 $$ Adding 3 to both sides gives: $$ 4 + 3 > 2 + 3 $$ $$ 7 > 5 $$ The result is a new inequality pointing in the same direction.
Example 2. Let’s start again with the same inequality: $$ 4 > 2 $$ This time, I subtract 5 from both sides: $$ 4 - 5 > 2 - 5 $$ $$ -1 > -3 $$ Once again, we end up with another inequality that maintains the same direction.
Multiplicative Property
If I multiply or divide both sides of an inequality by the same nonzero number, the direction of the inequality may stay the same or flip, depending on the sign of the number:
- It stays the same if the number is positive (c > 0): $$ a < b \Longleftrightarrow a \cdot c < b \cdot c $$
- It reverses if the number is negative (c < 0): $$ a < b \Longleftrightarrow a \cdot c > b \cdot c $$
Example. Consider the inequality $$ 4 > 2 $$ Multiplying both sides by 3 gives: $$ 4 \cdot 3 > 2 \cdot 3 $$ $$ 12 > 6 $$ The inequality remains true in the same direction.
Example 2. Let’s look at the inequality $$ 16 > 8 $$ Now, let’s divide both sides by -2: $$ \frac{16}{-2} > \frac{8}{-2} $$ $$ -8 > -4 $$ However, this last inequality is false because -8 is not greater than -4. Since we divided by a negative number, we must flip the inequality sign: $$ -8 < -4 $$ This gives us a true inequality, but in the opposite direction from the original.
Why Does Multiplying or Dividing by a Negative Number Reverse the Inequality?
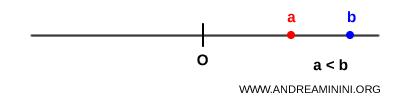
Let’s take two positive real numbers, $a > 0$ and $b > 0$, where $a < b$.
On the number line, this means the point representing $a$ lies to the left of the point representing $b$.
If I multiply both sides of the inequality $a < b$ by $-1$, I get $-a$ and $-b$.
This operation is equivalent to reflecting both points across the origin $O$ on the number line. Essentially, the points representing $a$ and $b$ flip to the opposite side of zero.
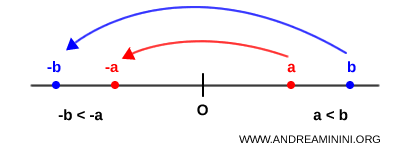
After this reflection, $-a$ is now positioned to the right of $-b$, because $a < b$ implies $-a > -b$.
So the order of the two numbers is reversed: what was smaller becomes greater, and vice versa.
Note. Multiplying or dividing by -1 is simply a special case of multiplying or dividing by any negative number. In general, multiplying or dividing both sides of an inequality by a negative flips the inequality sign because it reverses the order of the numbers on the number line.
Property of Reciprocals for Numbers with the Same Sign
If you take two like-signed numbers (both positive or both negative) that are nonzero, the inequality between their reciprocals points in the opposite direction to the inequality between the numbers themselves: $$ a > b \ \Longleftrightarrow \frac{1}{a} < \frac{1}{b} $$ This property doesn’t hold for numbers with opposite signs. For numbers with different signs, the inequality between their reciprocals retains the same direction as the original inequality.
Example. Consider the inequality $$ 4 > 2 $$ These are two nonzero numbers with the same sign, so the inequality between their reciprocals flips direction: $$ \frac{1}{4} < \frac{1}{2} $$ Example 2. Now consider this inequality: $$ -4 < 2 $$ In this case, the numbers have different signs - they’re unlike-signed - so the inequality between their reciprocals points in the same direction as the original: $$ - \frac{1}{4} < \frac{1}{2} $$
Proof
To prove this property, let’s consider two nonzero numbers $ a $ and $ b $.
- If the numbers have the same sign, their product is positive: $ ab > 0 $
- If the numbers have opposite signs, their product is negative: $ ab < 0 $
Let’s examine each case in turn.
A] Like-Signed Numbers
Suppose $ a > b $. Since both numbers have the same sign, their product $ ab > 0 $ is positive.
Dividing both sides of the inequality by a positive number doesn’t change its direction, so we have: $ \frac{a}{ab} > \frac{b}{ab} $.
$$ \frac{a}{ab} > \frac{b}{ab} \Rightarrow \frac{1}{b} > \frac{1}{a} \Rightarrow \frac{1}{a} < \frac{1}{b} $$
Thus, the inequality between their reciprocals is reversed: $ \frac{1}{a} < \frac{1}{b} $.
B] Unlike-Signed Numbers
Now suppose $ a > b $. Since the numbers have opposite signs, their product is negative: $ ab < 0 $.
Dividing both sides of the inequality by a negative number reverses the direction of the inequality, giving: $ \frac{a}{ab} < \frac{b}{ab} $.
$$ \frac{a}{ab} < \frac{b}{ab} \Rightarrow \frac{1}{b} < \frac{1}{a} \Rightarrow \frac{1}{a} > \frac{1}{b} $$
Therefore, the inequality between their reciprocals keeps the same direction as the original inequality: $ \frac{1}{a} > \frac{1}{b} $.
In this way, we’ve established the rule governing reciprocals, relying on the principle that multiplying or dividing both sides of an inequality by a negative number reverses its direction.
Exponentiation of Inequalities
When we raise two non-negative numbers to a power $ n \in \mathbb{N} $, the direction of the inequality remains the same: $$ a > b \Longleftrightarrow a^n > b^n $$ However, this property does not hold for negative numbers.
Example. Consider the numerical inequality $$ 4 > 2 $$ Raising both sides to the second power yields another inequality in the same direction: $$ 4^2 > 2^2 \Rightarrow 16 > 4 $$ Example. If one or both numbers are negative, this rule doesn’t necessarily apply, because the direction of the inequality depends on whether the exponent $ n $ is even or odd, as well as on the absolute values involved. For instance, consider $ -4 < -2 $. Squaring both sides reverses the inequality: $$ (-4)^2 < (-2)^2 \Rightarrow 16 > 4 $$ On the other hand, raising both sides to the third power preserves the original direction: $$ (-4)^3 < (-2)^3 \Rightarrow -64 < -8 $$
Proof
To prove this property, let’s take two non-negative numbers $ a > 0 $ and $ b > 0 $, with $ a > b $.
$$ a > b $$
We can express $ a $ as $ a = b + h $, where $ h = a - b $.
$$ b + h > b $$
Since $ a > b $, it follows that $ h = a - b > 0 $ is positive.
Now, let’s raise both sides of the inequality to the power $ n \in \mathbb{N} $:
$$ (b + h)^n > b^n $$
If $ n = 2 $ (even), we expand the square of the binomial:
$$ (b + h)^2 > b^2 $$
$$ b^2 + 2bh + h^2 > b^2 $$
It’s evident that the left-hand side is greater than the right-hand side because $ b^2 $ appears on both sides, and all the additional terms are positive, given that $ b > 0 $ and $ h > 0 $.
If $ n = 3 $ (odd), we expand the cube of the binomial:
$$ (b + h)^3 > b^3 $$
$$ b^3 + 3hb^2 + 3bh^2 + h^3 > b^3 $$
Once again, the left-hand side exceeds the right-hand side because $ b^3 $ appears on both sides, and every other term is positive, since $ b > 0 $ and $ h > 0 $.
Therefore, when $ a $ and $ b $ are non-negative, raising both sides of an inequality to any natural exponent $ n \in \mathbb{N} $, whether even or odd, does not change the direction of the inequality.
Adding Inequalities with the Same Direction
If I add two inequalities that point in the same direction, I get a new inequality that points in the same direction as well. $$ a > b \ , \ c > d \ \Longleftrightarrow a+c > b + d $$ This property does not hold if the numbers have opposite signs.
Example. Consider the inequalities $$ 4 > 2 $$ $$ 5 > 3 $$ Both inequalities point in the same direction. Adding them side by side gives: $$ 4+5 > 2+3 $$ The result is another inequality in the same direction: $$ 9 > 5 $$
Multiplying Inequalities with the Same Direction for Positive Numbers
If I multiply two inequalities that both point in the same direction and involve positive numbers, the result is another inequality in the same direction. $$ a > b \ , \ c > d \ \Longleftrightarrow a \cdot c > b \cdot d $$ This property does not hold when the numbers are negative.
Example. Consider the inequalities $$ 4 > 2 $$ $$ 5 > 3 $$ Both inequalities are in the same direction, and all terms are positive. Multiplying them side by side gives: $$ 4 \cdot 5 > 2 \cdot 3 $$ The result is another inequality pointing in the same direction: $$ 20 > 6 $$
And so on.
