Inequalities

An inequality is a statement that compares two algebraic or numerical expressions using an order relation ( < , > , ≤ , ≥ ). $$ P(x) > Q(x) $$

The symbols whose values we seek are the unknown variables of the inequality.

Here is a simple example.

$$ x+2 > 4 $$

In this case x is the unknown variable and the symbol ">" indicates the direction of the comparison.

Solving an inequality means determining all values of the unknown, called the solutions, that make the statement true.

Note. An inequality may involve one or several unknowns. It may have a single solution, no solutions or infinitely many. When more than one solution exists, we refer to the solution set.

Any inequality can be put into standard form by bringing all algebraic terms to one side of the comparison.

$$ P(x)+Q(x)>0 $$

Example. Take the inequality $$ x+2 > 4 $$. Rewriting it in standard form gives $$ x+2 - 4 > 0 $$ which simplifies to $$ x-2 > 0 $$

Order relations used in inequalities are shown below.

<	less than
>	greater than
≤	less than or equal to
≥	greater than or equal to

The symbols ≤ and ≥ allow equality, so the endpoint of the comparison is included in the solution set.

A practical example

Consider the inequality:

$$ x-2 > 0 $$

This inequality holds whenever x belongs to the open interval

$$ x \in (2,+\infty) $$

Every value x>2 satisfies the inequality because x-2 is strictly positive.

The corresponding solution set S is therefore

$$ S = \{ \ \forall \ x \in R \ | \ x>2 \ \} $$

Note. This reads: "for every (∀) x in the real numbers (R) such that (|) x is greater than 2".

Graphical representation of solution sets

To represent the solution set of an inequality, we typically use a number line where each point corresponds to a real number from -∞ to +∞.

• Draw a continuous segment to indicate all values of the variable that satisfy the inequality.
• Omit the portions of the number line that do not belong to the solution set.

 

Example. The inequality x-2>0 holds for all real numbers greater than 2. To represent this visually, draw a continuous line extending to the right from the point 2. This corresponds to the interval (2,∞).

The same approach applies even when the solution set involves negative numbers. For example, the inequality x+2>0 is satisfied for all x>-2, so the arrow begins at the point -2.

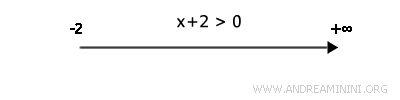
When marking the endpoints of intervals, we follow two conventions:

• A filled circle indicates that the endpoint is included in the solution set.
• An open circle indicates that the endpoint is excluded.

 

Example. The inequality x-2>0 is satisfied only for x>2. Since x=2 is not a solution, we mark this point with an open circle.

In contrast, the inequality x-4≤0 is satisfied for all x≤4. The endpoint x=4 belongs to the solution set and is marked with a filled circle.

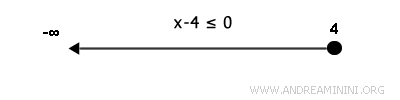
Solving an Inequality with a Sign Chart

For a continuous function, sign changes occur at specific points called zeros or roots, where the expression evaluates to zero.

Note. A root is a value of x that makes the expression equal to zero. To identify the roots, we replace the inequality with the corresponding equation and solve it. For example, $$ x - 2 > 0 $$ becomes $$ x - 2 = 0, $$ which yields x=2. Thus x=2 is a root of the inequality.

The first step is therefore to determine the roots.

Once the roots are known, we can analyze the sign of the expression on the intervals they define.

A sign chart provides a clear and efficient way to organize this analysis.

Example

We want to determine where the following expression is positive:

$$ x \cdot (x-2) > 0 $$

We begin by finding the zeros:

$$ x \cdot (x-2) = 0 $$

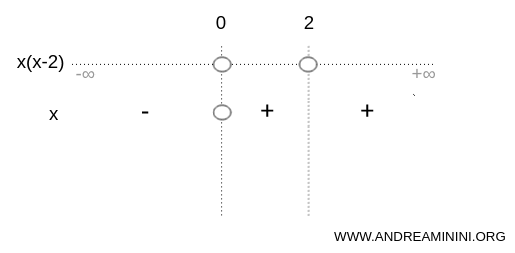
Since the expression is a product, it is zero at x=0 and x=2.

These values are the roots of the inequality.

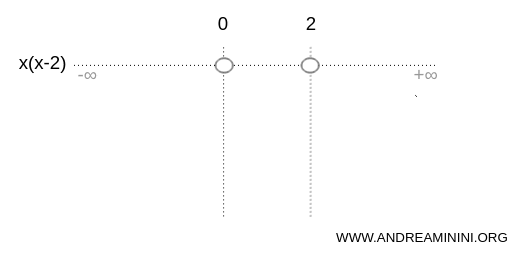
Note. In a graphical representation, a filled circle marks an included endpoint, while an open circle marks an excluded one. Here the circles are open because the inequality x(x-2)>0 is not satisfied at x=0 or x=2.

The roots partition the real line into three intervals:

$$ (-\infty , 0) \cup (0,2) \cup (2,+\infty) $$

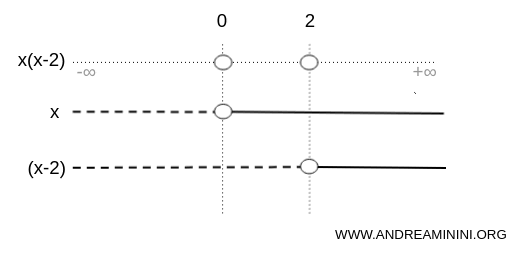
Because the expression is a product, we examine the sign of each factor, x and (x-2), on each interval.

The factor x is negative on (-∞,0), zero at x=0 and positive on (0,∞).

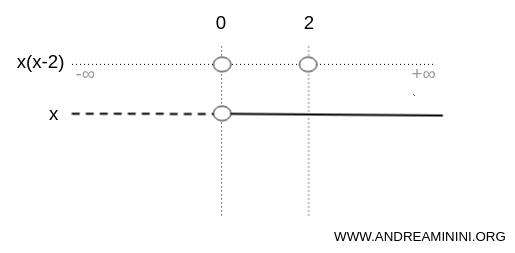
Note. In this sign chart, dashed segments represent negative values and solid segments represent positive values. A circle marks the point where the expression equals zero. A more compact alternative is to use + and - signs directly on each interval.

The factor (x-2) is negative on (-∞,2), zero at x=2 and positive on (2,+∞).

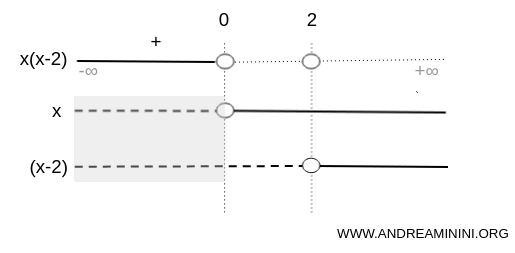
We now combine the signs to determine where the product is positive.

On (-\infty , 0), both factors are negative.

The product of two negative factors is positive, so x⋅(x-2)>0.

On (0,2), x is positive and (x-2) is negative.

Factors with opposite signs yield a negative product, so x⋅(x-2)<0.

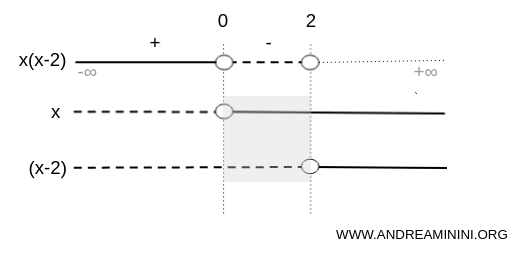
On (2,+\infty), both factors are positive.

A positive product results, so x⋅(x-2)>0.

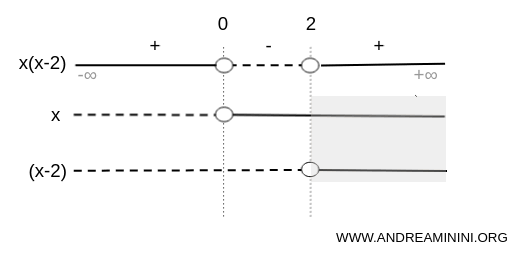
The inequality x(x-2)>0 is therefore satisfied on the intervals (-\infty ,0) and (2,+\infty).

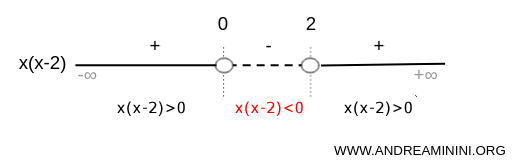
The solution set can be visualized on a number line by drawing a solid segment over the intervals where the inequality holds.

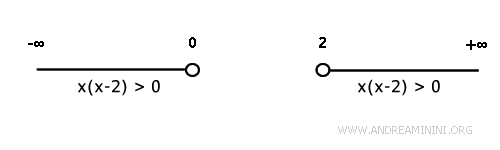
Using interval notation, the solution set is written as

$$ x \in \ ] -\infty , 0 [ \ \cup \ ] 2 , +\infty [ $$

where ∪ denotes the union of sets.

Note. An outward-facing bracket indicates an open endpoint, matching the open circle in the graphical representation. An inward-facing bracket indicates a closed endpoint. Parentheses are an equally standard notation for open intervals: $$ x \in (-\infty , 0) \cup (2 , +\infty). $$ The symbols ±∞ are always excluded from intervals because they are not real numbers.

Domain Restrictions

Domain restrictions specify the values of the variable for which an expression or inequality is defined.

Example

Consider the expression

$$ \frac{x}{x-2} $$

It is defined for all real x except x=2.

When x=2, the denominator is zero and division by zero is undefined.

The domain restriction is therefore

$$ x \in R - \{ 2 \} $$

that is, all real numbers except 2.

Degree of an Inequality

The degree of an inequality is the degree of the polynomial that appears in it, meaning the highest exponent of the variable.

Examples

$$ x - 1 > 0 $$ has degree 1 because the highest exponent of x is 1.

Note. First-degree inequalities are called linear inequalities.

$$ x^2 + x - 4 > 0 $$ has degree 2.

$$ 2x^3 - x + 1 > 0 $$ has degree 3.

Types of Inequalities

An inequality is classified as follows:

• polynomial inequality
  if the variable appears only in numerators of fractional expressions.

  Example $$ x^2 + \frac{2x}{3} - 3 > 0 $$

• rational inequality
  if the variable appears in denominators as well.

  Example $$ x^2 + \frac{2}{3x} - 3 > 0 $$

• linear inequality
  if the highest exponent of the variable is 1.

  Example $$ 2x - 3 > 2y - 7 $$

• numerical inequality
  if it contains only one variable and no parameters.

  Example $$ x^2 + 3x - 3 > 0 $$

• parametric inequality
  if it contains parameters or additional symbolic constants in addition to the variable.

  Example $$ kx^2 + 3k - 3 > 0 $$

And similar classifications follow.