Higher-Degree Polynomial Inequalities

To solve polynomial inequalities of degree greater than two, we factor the expression into linear and quadratic components and determine the sign of their product. This approach relies on understanding how each factor behaves over the real numbers.

In practice, synthetic division (Ruffini's rule) is one of the most efficient tools for factoring polynomials. Standard algebraic identities and, when appropriate, the introduction of an auxiliary variable can also simplify the process.

A variety of alternative factoring strategies exist, and the most effective method depends on the structure of the polynomial at hand.

A Worked Example

Consider the inequality

$$ 2x^3 - 3x^2 + 3x > 2 $$

We begin by rewriting it in standard form:

$$ 2x^3 - 3x^2 + 3x - 2 > 0 $$

We now apply synthetic division to factor the polynomial.

The associated equation 2x³ - 3x² + 3x - 2 = 0 has x = 1 as a root.

This allows us to express the polynomial as (x - 1) · Q(x), where Q(x) is a quadratic factor.

$$ \begin{array}{c|lcc|r} & 2 & -3 & 3 & -2 \\ 1 & & 2 & -1 & 2 \\ \hline & 2 & -1 & 2 & 0 \end{array} $$

This computation yields the factorization

$$ (x - 1) \cdot (2x^2 - x + 2) > 0 $$

We now examine the sign of each factor: the linear term (x - 1) and the quadratic term 2x² - x + 2. The quadratic is always positive because its discriminant is negative, so the sign of the product depends entirely on the sign of (x - 1).

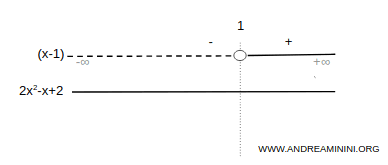
We then apply the sign rule to determine where the product of the factors is positive.

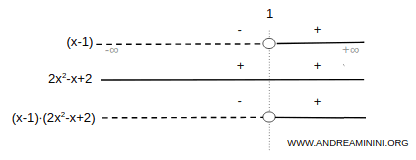
The inequality 2x³ - 3x² + 3x > 2 holds for every x > 1.