Irrational inequalities

An irrational inequality is an inequality in which the unknown variable appears inside a radical. Common forms are $$ \sqrt[n]{a(x)} > b(x) $$ and $$ \sqrt[n]{a(x)} < b(x) $$

Whenever the variable x appears under a radical sign, particular care is required, especially with regard to the index n of the root.

If n is odd

In this case, the inequality can be solved by raising both sides to the n-th power, since the function $$ t \mapsto t^n $$ is strictly increasing for odd values of n.

$$ \sqrt[n]{a(x)} > b(x) \ \ \ \text{is equivalent to} \ a(x) > b(x)^n $$

$$ \sqrt[n]{a(x)} < b(x) \ \ \ \text{is equivalent to} \ a(x) < b(x)^n $$

If n is even

When the index is even, the inequality must be solved by means of an equivalent system, because even-index roots are defined only for non-negative radicands.

$$ \sqrt[n]{a(x)} > b(x) \ \ \ \text{is equivalent to} \begin{cases} a(x) \ge 0 \\ \\ b(x)<0 \end{cases} \cup \begin{cases} b(x) \ge 0 \\ \\ a(x)>b(x)^n \end{cases} $$

$$ $$

$$ \sqrt[n]{a(x)} < b(x) \ \ \ \text{is equivalent to} \begin{cases} a(x) \ge 0 \\ \\ b(x)>0 \\ \\ a(x)< b(x)^n \end{cases} $$

A worked example

Consider the following inequality:

$$ \sqrt{5-x} < x+1 $$

This is an irrational inequality because the unknown x appears inside a radical.

The square root has index n = 2, which is positive and even.

For this reason, the inequality cannot be solved simply by squaring both sides.

To determine the solution, we must instead solve the system equivalent to the inequality.

$$ \begin{cases} a(x) \ge 0 \\ \\ b(x)>0 \\ \\ a(x)< b(x)^n \end{cases} $$

In this example, a(x)=5-x, b(x)=x+1, and n=2.

$$ \begin{cases} 5-x \ge 0 \\ \\ x+1>0 \\ \\ 5-x<(x+1)^2 \end{cases} $$

$$ \begin{cases} x \le 5 \\ \\ x>-1 \\ \\ 5-x<x^2+2x+1 \end{cases} $$

$$ \begin{cases} x \le 5 \\ \\ x>-1 \\ \\ -x-x^2-2x<1-5 \end{cases} $$

$$ \begin{cases} x \le 5 \\ \\ x>-1 \\ \\ -3x-x^2<-4 \end{cases} $$

$$ \begin{cases} x \le 5 \\ \\ x>-1 \\ \\ x^2+3x>4 \end{cases} $$

The solution sets of the individual inequalities are illustrated below.

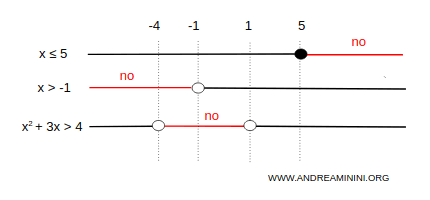
Note. The first two inequalities, x≤5 and x>-1, are immediate. The inequality $$ x^2+3x>4 $$ is a quadratic inequality, which can be rewritten as $$ x^2+3x-4>0 $$ This corresponds to a parabola opening upward. Its roots are $$ x = \frac{-3 \pm \sqrt{25}}{2} = \frac{-3 \pm 5}{2} = \begin{cases} x_1 = \frac{-3-5}{-2} = -4 \\ \\ x_2 = \frac{-3+5}{2} = 1 \end{cases} $$ Therefore, the inequality x²+3x-4>0 is satisfied on the interval (-∞;-4)∪(1;∞).

The system is solved where all inequalities are satisfied simultaneously.

In this case, all conditions are met on the interval (1,5].

Therefore, the system of inequalities is satisfied when

$$ 1 < x \le 5 $$

This interval is also the solution of the original inequality.

The proof

1] The inequality ⁿ√a(x)>b(x) with positive even index n

Consider an irrational inequality with a positive, even index n:

$$ \sqrt[n]{a(x)} > b(x) $$

The explicit expressions of a(x) and b(x) are not specified.

However, a root with an even index is defined only when the radicand is non-negative.

Hence, the domain condition is a(x)≥0.

$$ \begin{cases} \sqrt[n]{a(x)} > b(x) \\ \\ a(x) \ge 0 \end{cases} $$

The function b(x) may be negative, zero, or positive. We therefore analyze the cases separately.

• If b(x) ≥ 0 $$ \begin{cases} \sqrt[n]{a(x)} > b(x) \\ \\ a(x) \ge 0 \\ \\ b(x) \ge 0 \end{cases} $$ Since both a(x) and b(x) are non-negative, the inequality holds if and only if a(x)>b(x)ⁿ. The corresponding solution set is $$ S_1 = \begin{cases} a(x) \ge 0 \\ \\ b(x)>0 \\ \\ a(x)>b(x)^n \end{cases} $$ The condition a(x)≥0 is redundant here, as it is already implied by a(x)>b(x)ⁿ, given that b(x)ⁿ≥0. Thus, the system can be simplified to $$ S_1 = \begin{cases} b(x)>0 \\ \\ a(x)>b(x)^n \end{cases} $$
• If b(x)<0 $$ \begin{cases} \sqrt[n]{a(x)} > b(x) \\ \\ a(x) \ge 0 \\ \\ b(x)<0 \end{cases} $$ Since a(x) is non-negative while b(x) is negative, the inequality is automatically satisfied. The corresponding solution set is $$ S_2 = \begin{cases} a(x) \ge 0 \\ \\ b(x)<0 \end{cases} $$

Consequently, the solutions of the original inequality belong to the union of S₁ and S₂.

$$ S_1 \cup S_2 = \begin{cases} b(x)>0 \\ \\ a(x)>b(x)^n \end{cases} \cup \begin{cases} a(x) \ge 0 \\ \\ b(x)<0 \end{cases} $$

2] The inequality ⁿ√a(x)< b(x) with positive even index n

Consider an irrational inequality with a positive, even index n:

$$ \sqrt[n]{a(x)} < b(x) $$

The explicit expressions of a(x) and b(x) are not specified.

As before, an even-index root requires a non-negative radicand.

Therefore, the domain condition is a(x)≥0.

$$ \begin{cases} \sqrt[n]{a(x)} < b(x) \\ \\ a(x) \ge 0 \end{cases} $$

Since a(x)≥0, the inequality can only be satisfied if b(x)>0.

When both a(x) and b(x) are positive, both sides of the inequality may be raised to the n-th power without altering its direction.

Therefore, the solution set is

$$ S = \begin{cases} a(x) \ge 0 \\ \\ b(x)>0 \\ \\ a(x)< b(x)^n \end{cases} $$

And similarly for related cases.