Rational Inequalities
A rational inequality is an inequality in which the variable appears in the denominator of a rational expression. Common examples include $$ \frac{A(x)}{B(x)} > 0 $$ and $$ \frac{A(x)}{B(x)} < 0 $$
How to solve a rational inequality
Rational inequalities are solved through a standard and systematic procedure.
- Rewrite the inequality in standard form $$ \frac{A(x)}{B(x)} > k $$ and then reduce it to $$ \frac{A(x)}{B(x)} - k > 0 $$
- Determine the domain of the expression by requiring the denominator B(x) to be nonzero $$ B(x) \ne 0 $$
- Study the sign of the numerator A(x) and the denominator B(x) separately.
- Combine the results using sign rules to identify where the rational expression is positive or negative.
Note. The same method applies when strict inequalities are replaced by non-strict ones, such as $$ \frac{A(x)}{B(x)} \ge 0 $$ or $$ \frac{A(x)}{B(x)} \le 0 $$
A worked example
Example 1
Consider the following rational inequality.
$$ \frac{5x-1}{x-3} \ge 1 $$
Begin by rewriting the inequality in standard form, moving all terms to the left-hand side.
$$ \frac{5x-1}{x-3} -1 \ge 0 $$
$$ \frac{5x-1-(x-3)}{x-3} \ge 0 $$
$$ \frac{5x-1-x+3}{x-3} \ge 0 $$
$$ \frac{4x+2}{x-3} \ge 0 $$
The denominator must not be zero, since division by zero is undefined.
We therefore impose the domain condition of the inequality.
$$ x-3 \ne 0 $$
$$ x \ne 3 $$
For clarity, the symbol ∄, indicating exclusion from the domain, is recorded on the sign chart, which will be completed step by step.
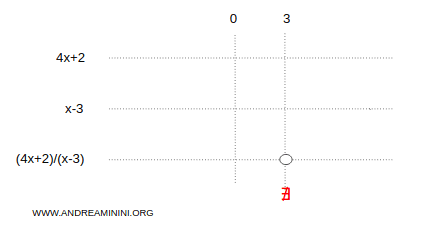
Next, analyze the sign of the polynomial in the numerator.
$$ 4x+2 \ge 0 $$
$$ x \ge \frac{-2}{4} $$
$$ x \ge \frac{-1}{2} $$
The numerator is nonnegative for all values of x greater than or equal to -1/2.
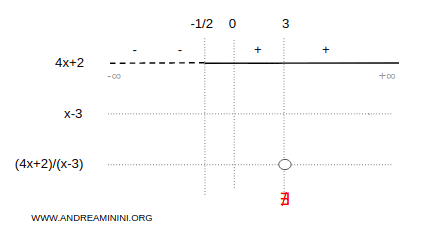
Now examine the sign of the denominator.
$$ x-3 \ge 0 $$
$$ x \ge 3 $$
The denominator is positive for all values of x greater than 3.
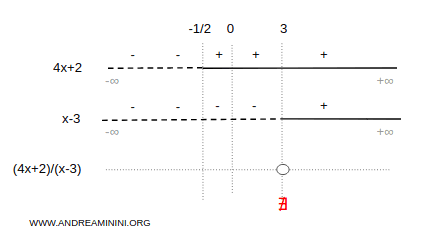
At this stage, combine the two sign analyses to determine the sign of the rational expression.
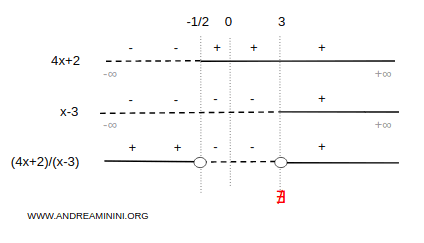
It follows that the original inequality is satisfied on the intervals (-∞, -1/2] and (3,+∞).
$$ x \le - \frac{1}{2} \ ∨ \ x \gt 3 $$
On these intervals, the rational expression is greater than or equal to zero.
Example 2
Consider the following rational inequality.
\[ \frac{x - 3}{x + 2} > 1 \]
Move all terms to the left-hand side.
\[ \frac{x - 3}{x + 2} - 1 > 1 -1 \]
\[ \frac{x - 3}{x + 2} - 1 > 0 \]
Rewrite the constant \( 1 \) as a fraction with denominator \( x + 2 \).
\[ \frac{x - 3}{x + 2} - \frac{x + 2}{x + 2} > 0 \]
\[ \frac{x - 3 - (x + 2)}{x + 2} > 0 \]
\[ \frac{x - 3 - x - 2}{x + 2} > 0 \]
\[ \frac{-5}{x + 2} > 0 \]
The inequality is now expressed as a single rational expression, making its sign easy to analyze.
For the expression to be defined, the denominator must be nonzero.
\[ x+2 \ne 0 \]
\[ x+2 -2 \ne 0 -2 \]
\[ x \ne -2 \]
The value \( x = -2 \) is therefore excluded, since it would make the denominator of the fraction $ \frac{-5}{x + 2} > 0 $ equal to zero and the expression undefined.

A rational expression is positive when its numerator and denominator have the same sign.
Because the numerator is \( -5 \), which is strictly negative, the fraction $ \frac{-5}{x + 2} > 0 $ is positive only when the denominator is also negative, that is, when:
\[ x + 2 < 0 \]
\[ x < -2 \]
Thus, the rational inequality is satisfied only when the denominator is negative. The solution set is:
\[ x < -2 \]
Excluding the value \[ x = -2 \], where the expression is undefined, the inequality is positive for all \( x < -2 \) and negative for all \( x > -2 \).
Solved Exercises
Below are three fully worked exercises on rational inequalities, arranged by increasing level of difficulty. Each solution is presented step by step, in accordance with standard methods used in undergraduate mathematics.
- Basic exercises. Introduce rational inequalities, with particular attention to domain restrictions.
- Intermediate exercises. Focus on inequalities involving quadratic polynomials and factorization techniques.
- Advanced exercises. Address inequalities with parameters and more subtle analytical conditions.
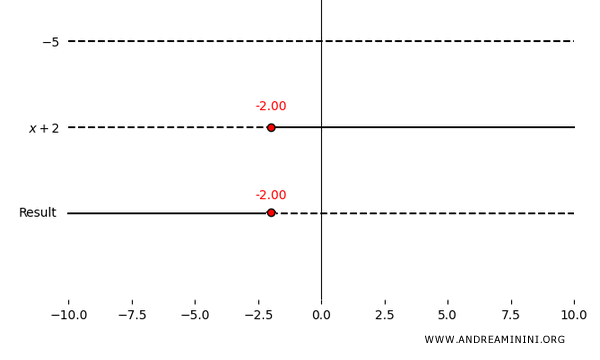
Exercise 1 - Basic Level
Solve the following rational inequality.
\[ \frac{x + 2}{x - 3} > 0 \]
The first step is to determine the domain.
The denominator must be nonzero, so the value \( x - 3 = 0 \Rightarrow x \neq 3 \) is excluded.
Next, we analyze the sign of the rational expression. A rational expression can change sign only at points where either the numerator or the denominator vanishes.
- \( x + 2 = 0 \Rightarrow x = -2 \)
- \( x - 3 = 0 \Rightarrow x = 3 \), which is excluded from the domain
We now construct the sign chart.
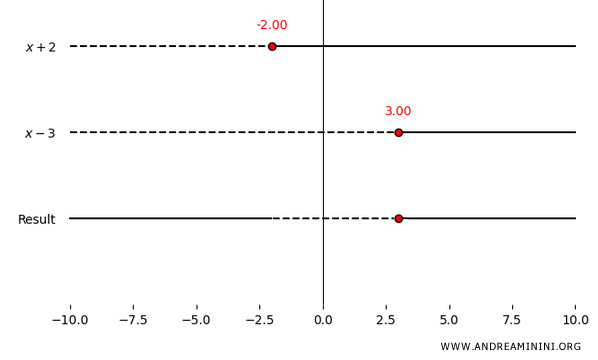
For \( x < -2 \), the numerator is negative while the denominator is positive, so the fraction is negative.
For \( -2 < x < 3 \), both the numerator and the denominator are positive, so the fraction is positive.
For \( x > 3 \), the numerator is positive and the denominator is negative, so the fraction is negative.
Therefore, the solution set is:
\[ x \in (-2, 3) \]
Excluding the value \( x = 3 \), where the denominator vanishes, the inequality holds on the interval (-2, 3) and fails elsewhere.
Exercise 2 - Intermediate Level
Solve the rational inequality
\[ \frac{x^2 - 4}{x^2 - x - 6} \leq 0 \]
The numerator factors as \( x^2 - 4 = (x - 2)(x + 2) \), which vanishes at \( x = \pm 2 \).
\[ \frac{(x - 2)(x + 2)}{x^2 - x - 6} \leq 0 \]
The denominator factors as \( x^2 - x - 6 = (x - 3)(x + 2) \).
\[ \frac{x^2 - 4}{(x - 3)(x + 2)} \leq 0 \]
Thus, the denominator vanishes at \( x = 3 \) and \( x = -2 \). At these points, the rational expression is undefined due to division by zero.
We now determine the sign of the expression by examining each factor.
Constructing the sign chart:
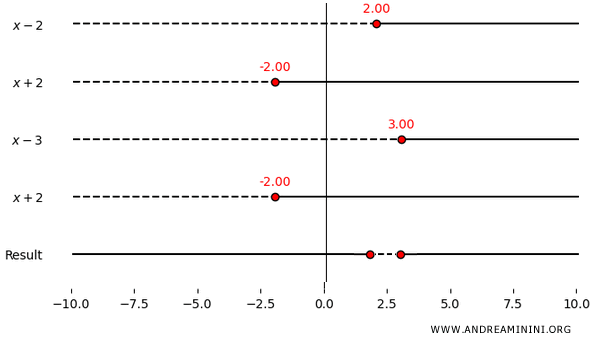
In this case, apart from the excluded points \( x = -2 \) and \( x = 3 \), the inequality is satisfied only on the interval \( (2, 3) \), where the expression is nonpositive.
\[ (2, 3) \]
Outside this interval, the rational expression is strictly positive.
Exercise 3 - Advanced Level
In this exercise, we solve the following rational inequality.
\[ \frac{x^2 - 3x + p}{x - 1} > 0 \]
This is a parametric inequality, since \( p \) is a real parameter.
We begin by determining the domain of the general solution.
The denominator imposes the condition \( x - 1 \neq 0 \), hence \( x \neq 1 \).
The numerator \( x^2 - 3x + p \) is a quadratic trinomial. Its zeros are obtained using the quadratic formula.
\[ x = \frac{3 \pm \sqrt{9 - 4p}}{2} \]
For the numerator to change sign, the discriminant must be nonnegative. This requires \( 9 - 4p \geq 0 \).
$$ 9 - 4p \geq 0 $$
$$ -4p \geq -9 $$
$$ (-1)\cdot(-4p) \geq -9\cdot(-1) $$
$$ 4p \leq 9 $$
$$ p \leq \frac{9}{4} $$
Therefore, real roots of the numerator exist only when $ p \leq \frac{9}{4} $.
Depending on the value of \( p \), the inequality admits different solution sets, which must be examined case by case.
The simplest case occurs when \( p = 0 \). The corresponding sign chart is shown below.
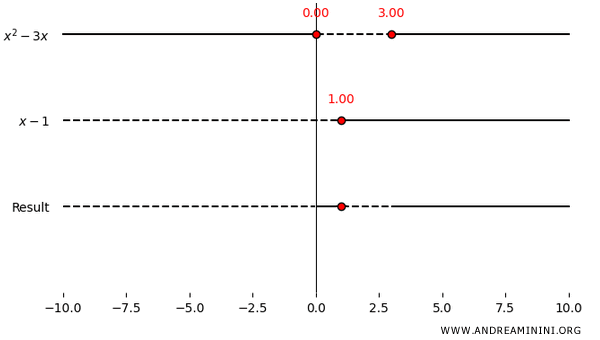
In the general case \( p \ne 0 \), we analyze when the numerator is positive.
\[ x^2 - 3x + p > 0 \]
If $ p \leq \frac{9}{4} $ and $ p \ne 0 $, the quadratic polynomial has two distinct real roots \( x_1 < x_2 \).
\[ x = \frac{3 \pm \sqrt{9 - 4p}}{2} = \begin{cases} x_1 = \frac{3 - \sqrt{9 - 4p}}{2} \\ \\ x_2 = \frac{3 + \sqrt{9 - 4p}}{2} \end{cases} \]
Since the coefficient of $ x^2 $ is positive, the parabola opens upward. Consequently, the polynomial $ x^2 - 3x + p $ is negative on the interval (x_1, x_2) and positive on the intervals $ (-\infty, x_1) $ and $ (x_2, +\infty) $.
Taking the denominator \( x - 1 \) into account, we obtain the following sign table.
| Interval | \( x < x_1 \) | \( x_1 < x < 1 \) | \( 1 < x < x_2 \) | \( x > x_2 \) |
|---|---|---|---|---|
| \( x^2 - 3x + p \) (Numerator) | + | - | - | + |
| \( x - 1 \) (Denominator) | - | - | + | + |
| Sign of the fraction | - | + | - | + |
In conclusion, the inequality $ \frac{x^2 - 3x + p}{x - 1} > 0 $ is satisfied on the following set:
$$ (x_1 , 1 ) \cup ( x_2 , +\infty ) $$
And so on.
