Linear Inequalities

Linear inequalities are expressions of the form $$ ax + b > 0 $$ or $$ ax + b < 0, $$ where the coefficient $ a \ne 0 $ ensures that the expression is genuinely linear.

The underlying polynomial has degree one.

The variable appears only to the first power.

Note. The inequality symbol may also include equality, as in $$ ax + b \ge 0 $$ or $$ ax + b \le 0. $$

A practical example

Consider the linear inequality

$$ 3x < 6 $$

This is a linear inequality because $ x $ is raised to the first power.

Note. It can also be written in standard form: $$ 3x - 6 < 0. $$ Both forms express the same inequality.

To solve the inequality, we determine all values of the variable that satisfy the stated order relation.

We isolate $ x $ by dividing both sides by three:

$$ \frac{3x}{3} < \frac{6}{3} $$

which gives

$$ x < 2. $$

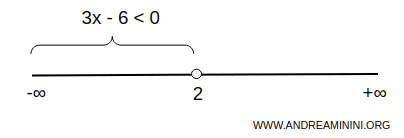
The solution set $ S $ therefore consists of all real numbers less than 2:

$$ S = \{ x \in \mathbb{R} \mid x < 2 \}. $$

Graphically, this corresponds to

solution set illustrated on a number line

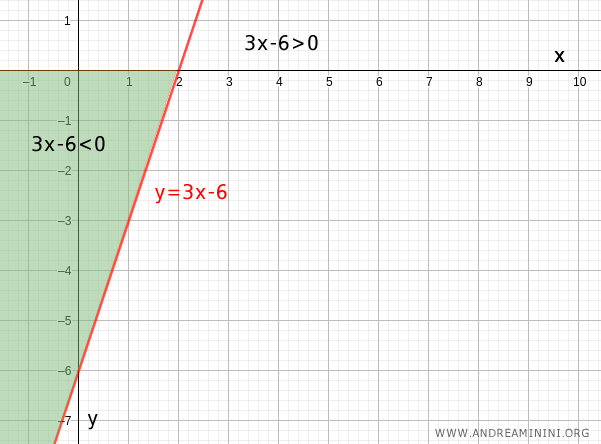
Note. A graphical approach leads to the same conclusion. The inequality $$ 2x - 6 < 0 $$ corresponds to the linear function y = 2x - 6. The line has slope 2 and y-intercept at (0, -6). It crosses the x-axis at (2, 0). From the graph, it is clear that the line takes negative values, that is $ y = 2x - 6 < 0 $, for all x-values less than 2.
graph of the associated linear function illustrating the inequality

And so on.