Quadratic Inequalities
A quadratic inequality is expressed in standard form as $$ ax^2 + bx + c > 0 $$ or $$ ax^2 + bx + c < 0 $$ where a, b, and c are real coefficients and a≠0.
The polynomial has degree two.
In other words, the variable appears squared.
Note. Quadratic inequalities may also be written using non strict inequalities: $$ ax^2+bx+c \ge 0 $$ or $$ ax^2+bx+c \le 0 $$. The analytical approach remains the same.
Solving a Quadratic Inequality
To solve an inequality in the form
$$ ax^2+bx+c > 0 $$
I begin by examining the associated quadratic equation:
$$ ax^2+bx+c = 0 $$
The first step is to determine the orientation of the parabola defined by the corresponding quadratic function.
- a > 0
The parabola opens upward. - a < 0
The parabola opens downward.
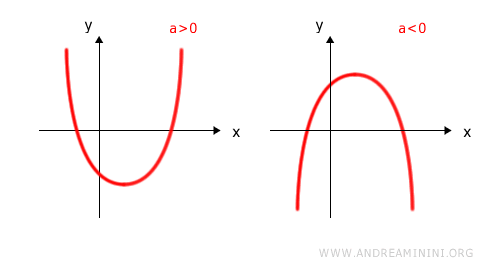
Note. The concavity immediately reveals whether the function’s minimum or maximum lies between its real roots or toward the ends of the real axis.
Next I determine whether the equation has real roots, that is, x1 and x2 where the graph intersects the x axis.
$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
The nature of the roots depends on the discriminant.
1] Positive Discriminant
If Δ = b2 - 4ac > 0, the equation has two distinct real roots.
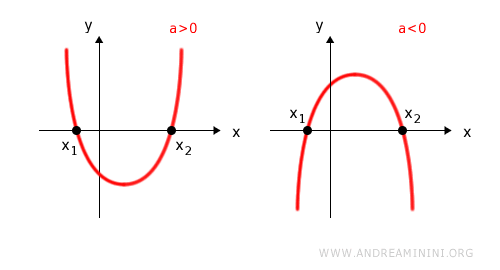
In this case the inequality always admits a non empty solution set.
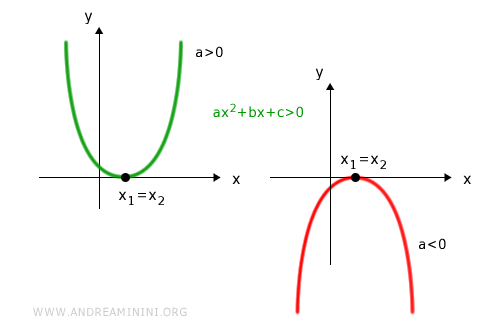
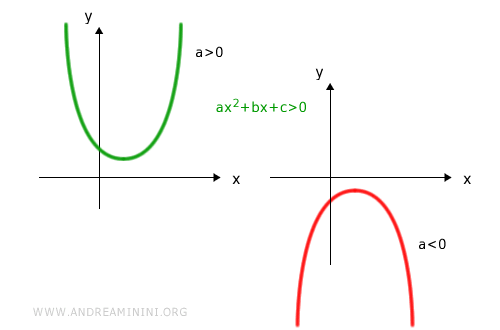
- For ax2 + bx + c > 0:
- the solution set is (-∞, x1) ∪ (x2, +∞) if the parabola opens upward (a > 0)
- the solution set is (x1, x2) if the parabola opens downward (a < 0)
- the solution set is (x1, x2) when a > 0
- the solution set is (-∞, x1) ∪ (x2, +∞) when a < 0
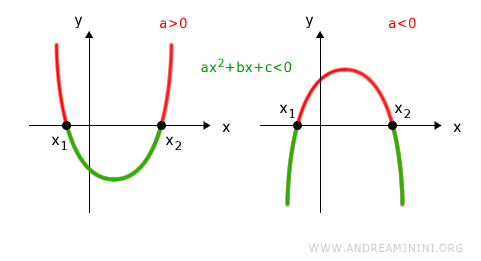
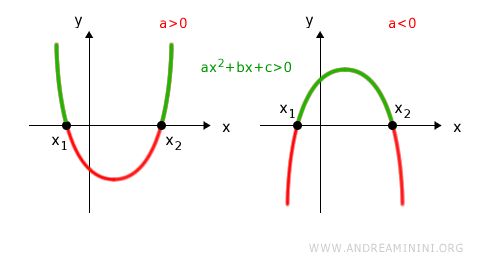
For ax2 + bx + c < 0:
2] Zero Discriminant
If Δ = 0, the quadratic equation has a single real root of multiplicity two.
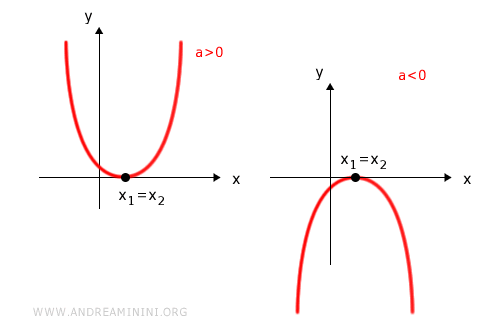
Depending on concavity, the inequality may hold everywhere except at the root or fail everywhere.
- For ax2 + bx + c > 0:
- the inequality holds for all real x except the root when a > 0
- there are no solutions when a < 0
- no solutions exist when a > 0
- the inequality holds for all real x except the root when a < 0
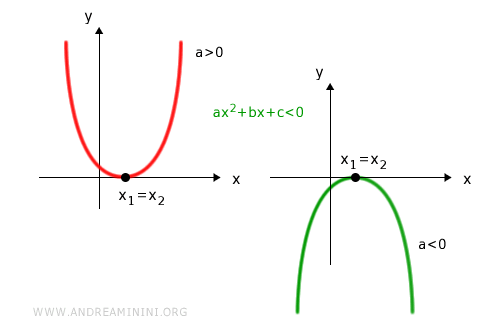
For ax2 + bx + c < 0:
3] Negative Discriminant
If Δ < 0, the quadratic has no real roots and the graph does not intersect the x axis.
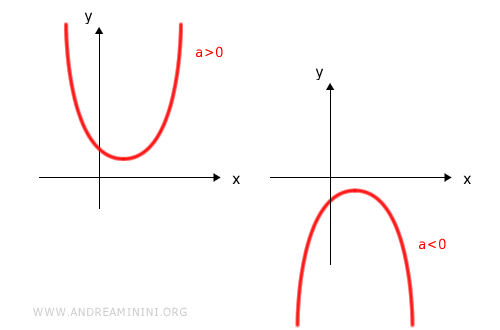
In this situation the inequality either holds for all real numbers or has no solutions, depending solely on concavity.
- For ax2 + bx + c > 0:
- the inequality is true for all real x when a > 0
- there are no solutions when a < 0
- no solutions exist when a > 0
- the inequality is true for all real x when a < 0
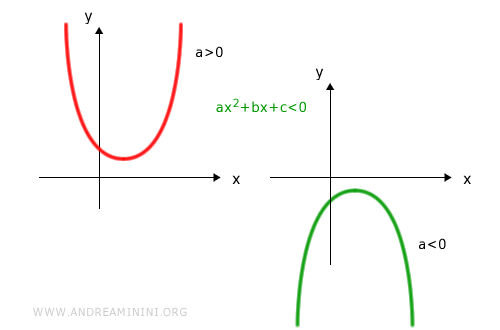
For ax2 + bx + c < 0:
A Fully Worked Example
Consider the inequality
$$ 2x^2 - x - 1 < 0 $$
First examine the associated equation:
$$ 2x^2 - x - 1 = 0 $$
Since a = 2 is positive, the parabola opens upward.
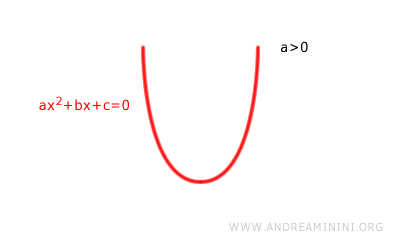
Note. At this stage whether the parabola crosses the x axis is not yet known, so the axes are omitted. The only relevant point is the upward concavity.
Now compute the discriminant:
$$ \Delta = b^2 - 4ac = (-1)^2 - 4(2)(-1) = 1 + 8 = 9 $$
The discriminant is positive, so the equation has two distinct real roots.
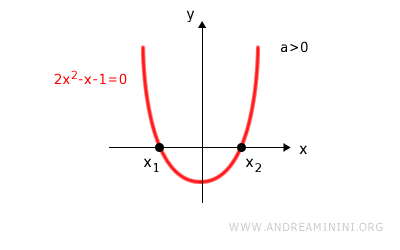
For an upward opening parabola, the function takes negative values between the two roots, so the inequality is satisfied precisely on that interval.
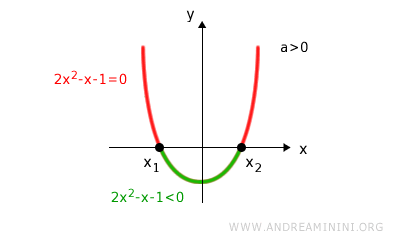
Compute the exact roots:
$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
$$ x = \frac{-(-1) \pm \sqrt{(-1)^2 - 4 \cdot 2 \cdot (-1)}}{4} = \frac{1 \pm \sqrt{9}}{4} = \frac{1 \pm 3}{4} $$
The roots are:
$$ x = \begin{cases} x_1 = \frac{1 - 3}{4} = -\frac{1}{2} \\ \\ x_2 = \frac{1 + 3}{4} = 1 \end{cases} $$
Thus the solution set of the inequality is:
$$ (x_1 ; x_2) = \left( -\frac{1}{2} ; 1 \right) $$
Graphically:
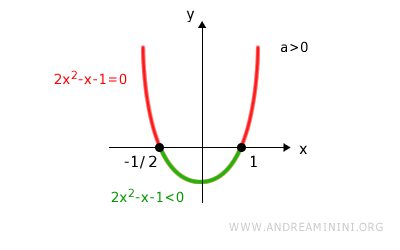
The solution set is
$$ S = \{ x \in \mathbb{R} \mid -\frac{1}{2} < x < 1 \} $$
This is read as: all real x such that x is greater than minus one half and less than one.
