Inequalities with absolute value
To solve an inequality involving the absolute value (modulus) of the unknown variable x, such as $$ |P(x)| > Q(x) $$, the absolute value must be removed by rewriting the inequality in an equivalent form.
For example, consider an inequality of the form
$$ |P(x)| > Q(x) $$
Inequalities of this type are solved by following a standard and systematic procedure.
- First, determine the sign of the expression P(x) inside the absolute value.
- Once the intervals where P(x) is nonnegative and negative have been identified, rewrite the original inequality as two separate systems of inequalities.
- The first system corresponds to the case P(x) ≥ 0: $$ \begin{cases} P(x) \ge 0 \\ \\ P(x) > Q(x) \end{cases} $$
- The second system corresponds to the case P(x) < 0: $$ \begin{cases} P(x) < 0 \\ \\ -P(x) > Q(x) \end{cases} $$ Here, -P(x) appears in the second inequality because of a fundamental property of absolute values. When P(x) < 0, its absolute value satisfies |P(x)| = -P(x).
- The solution of the original inequality is obtained by taking the union of the solution sets of the two systems.
Note. More generally, if k is any positive real number, k > 0, then $$ |P(x)| < k \Rightarrow -k < P(x) < k $$ $$ |P(x)| > k \Rightarrow P(x) < -k \text{ or } P(x) > k $$
A worked example
Example 1
In the following inequality, the unknown x appears inside an absolute value.
$$ |3x-4| \ge 2x+5 $$
I begin by analyzing the sign of the expression P(x) = 3x - 4 inside the absolute value.
$$ 3x-4 \ge 0 $$
$$ x \ge \frac{4}{3} $$
The expression P(x) = 3x - 4 is therefore nonnegative for all x ≥ 4/3.
At this stage, I construct two systems of inequalities, one corresponding to x ≥ 4/3 and the other to x < 4/3.
The first system
If x ≥ 4/3, the absolute value can be removed without changing the sign of the expression.
$$ \begin{cases} x \ge \frac{4}{3} \\ \\ 3x-4 \ge 2x+5 \end{cases} $$
$$ \begin{cases} x \ge \frac{4}{3} \\ \\ 3x-2x \ge 5+4 \end{cases} $$
$$ \begin{cases} x \ge \frac{4}{3} \\ \\ x \ge 9 \end{cases} $$
The solutions of the first system are those values of x belonging to the interval [9, +∞).
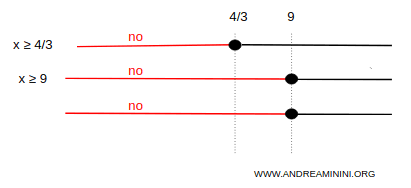
The second system
If x < 4/3, removing the absolute value requires replacing P(x) with its opposite, -P(x).
$$ \begin{cases} x < \frac{4}{3} \\ \\ -(3x-4) \ge 2x+5 \end{cases} $$
$$ \begin{cases} x < \frac{4}{3} \\ \\ -3x+4 \ge 2x+5 \end{cases} $$
$$ \begin{cases} x < \frac{4}{3} \\ \\ -5x \ge 1 \end{cases} $$
$$ \begin{cases} x < \frac{4}{3} \\ \\ x \le - \frac{1}{5} \end{cases} $$
The solutions of the second system are those values of x in the interval (-∞, -1/5].
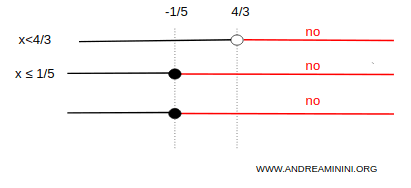
The solution set of the original inequality is given by the union of the solution sets of the two systems.
$$ ( -\infty, - \frac{1}{5} ] \cup [ 9 , + \infty) $$
Therefore, the inequality is satisfied precisely when
$$ x \le - \frac{1}{5} \text{ or } x \ge 9 $$
Example 2
I now turn to the inequality
$$ |1-x| < 6 $$
In this case, the expression inside the absolute value is P(x) = 1 - x, while Q(x) = 6.
I eliminate the absolute value by rewriting the original inequality as two systems.
$$ \begin{cases} P(x) \ge 0 \\ \\ P(x) < Q(x) \end{cases} \ \ \ \ \ \ \begin{cases} P(x) < 0 \\ \\ -P(x) < Q(x) \end{cases} $$
I then solve each system separately.
The first system
I solve the first system using P(x) = 1 - x and Q(x) = 6.
$$ \begin{cases} P(x) \ge 0 \\ \\ P(x) < Q(x) \end{cases} $$
$$ \begin{cases} 1-x \ge 0 \\ \\ 1-x < 6 \end{cases} $$
$$ \begin{cases} -x \ge -1 \\ \\ -x < 5 \end{cases} $$
$$ \begin{cases} x \le 1 \\ \\ x > -5 \end{cases} $$
The first system is satisfied for all x such that x > -5 and x ≤ 1, that is, for x in the interval (-5, 1].
$$ x \in (-5, 1] $$
The second system
I solve the second system using P(x) = 1 - x and Q(x) = 6.
$$ \begin{cases} P(x) < 0 \\ \\ -P(x) < Q(x) \end{cases} $$
$$ \begin{cases} 1-x < 0 \\ \\ -(1-x) < 6 \end{cases} $$
$$ \begin{cases} -x < -1 \\ \\ x-1 < 6 \end{cases} $$
$$ \begin{cases} x > 1 \\ \\ x < 7 \end{cases} $$
The second system is satisfied for all x such that x > 1 and x < 7, that is, for x in the interval (1, 7).
$$ x \in (1, 7) $$
The solution of the inequality
The solution of the original inequality is the union of the solutions of the two systems.
$$ x \in (-5, 1] \cup (1, 7) $$
$$ x \in (-5, 7) $$
In other words, the solution consists of all real numbers strictly between -5 and 7.
$$ -5 < x < 7 $$
And so on.
