Quadratic Equations

A quadratic equation is an equation in which the highest power of the unknown variable is two. $$ ax^2 + bx + c = 0 $$

The general form of a quadratic equation is:

$$ ax^2 + bx + c = 0 $$

The variable x is the unknown. In a quadratic equation, the greatest exponent of x is 2.

The letters a, b, and c are called the coefficients, and they may be either positive or negative numbers.

• a = first coefficient
• b = second coefficient
• c = third coefficient

The coefficient c is also known as the constant term.

Note. The coefficient a must always be nonzero: $$ a \ne 0 $$. If a were zero, the equation would no longer be quadratic but linear. The coefficients b and c, however, may be zero. For instance, if b=0, the quadratic equation becomes $$ ax^2 + c = 0 $$

When the coefficient a equals 1, the equation is said to be in standard form:

$$ x^2 + bx + c = 0 $$

Note. To obtain the standard form, divide the entire quadratic equation by a: $$ \frac{ax^2 + bx + c}{a} = \frac{0}{a} $$ $$ \frac{ax^2}{a} + \frac{bx}{a} + \frac{c}{a} = 0 $$ $$ x^2 + \frac{b}{a}x + \frac{c}{a} = 0 $$

If all three coefficients a, b, and c are nonzero (a≠0, b≠0, c≠0), the equation is called a complete quadratic equation.

If one or two of the coefficients (b, c) are zero, the equation is called an incomplete quadratic equation.

More precisely, depending on which coefficients are zero, an incomplete quadratic equation can be classified as:

• spurious equation
  when the constant term is zero (c=0) and the second coefficient is not (b≠0): $$ x^2 + bx = 0 $$
• pure equation
  when the constant term is nonzero (c≠0) and the second coefficient is zero (b=0): $$ x^2 + c = 0 $$
• monomial equation
  when both the constant term (c=0) and the second coefficient (b=0) are zero: $$ ax^2 = 0 $$

Solutions of a Quadratic Equation

Solving a quadratic equation means finding the values of x that satisfy it.

A solution of a quadratic equation is a value that, when substituted for x, makes the equation true: $$ ax^2 + bx + c = 0 $$

The solutions of a quadratic equation are also known as its roots.

A quadratic equation can have up to two solutions, though it may have only one or even none.

Example

Consider the quadratic equation:

$$ 2x^2 - 4x - 6 $$

Let's test x = 3 as a possible solution:

$$ 2·(3)^2 - 4·(3) - 6 = $$

$$ 2·9 - 12 - 6 = $$

$$ 18 - 18 = 0 $$

This confirms that x = 3 is a solution. The equation also has another root, x = -1:

$$ 2·(-1)^2 - 4·(-1) - 6 = $$

$$ 2·1 + 4 - 6 = $$

$$ 2 - 2 = 0 $$

However, it's not always possible to find the roots by inspection.

Fortunately, there's a straightforward numerical method that lets us determine all the solutions quickly and efficiently.

How to find all the solutions of a quadratic equation

To find the roots of a quadratic equation, apply the quadratic formula: $$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$ For a detailed derivation of this formula.

The expression under the square root is called the discriminant and is represented by the Greek capital letter Delta (Δ):

$$ \Delta = b^2 - 4ac $$

Note. If the coefficient b is even, you can use the simplified quadratic formula: $$ x = \frac{-\frac{b}{2} \pm \sqrt{(\frac{b}{2})^2 - ac}}{a} $$ It's obtained by dividing both numerator and denominator by 2: $$ x = \frac{-b \cdot \frac{1}{2} \pm \sqrt{b^2 - 4ac} \cdot \frac{1}{2}}{2a \cdot \frac{1}{2}} $$ $$ x = \frac{-\frac{b}{2} \pm \sqrt{(b^2 - 4ac)\cdot \frac{1}{4}}}{2} $$ $$ x = \frac{-\frac{b}{2} \pm \sqrt{\frac{b^2}{4} - \frac{4ac}{4}}}{a} $$ $$ x = \frac{-\frac{b}{2} \pm \sqrt{(\frac{b}{2})^2 - ac}}{a} $$

The sign of the discriminant determines how many real solutions the quadratic equation has:

• If Δ>0, the equation has two distinct real roots, x₁ and x₂.
• If Δ=0, the equation has one real root, or equivalently, two identical real roots x₁ = x₂ (a double root).
• If Δ<0, the equation has no real solutions.

  Note. When the discriminant is less than zero (Δ<0), the equation still has solutions in the set of complex numbers, which appear as complex conjugate pairs.

Graphically, a quadratic equation represents a parabola whose axis of symmetry is the vertical line:

$$ x = -\frac{b}{2a} $$

and whose vertex is the point:

$$ V \begin{pmatrix} -\frac{b}{2a} \ ; \ -\frac{b^2 - 4ac}{4a} \end{pmatrix} $$

The roots (solutions) correspond to the points where the parabola intersects the x-axis.

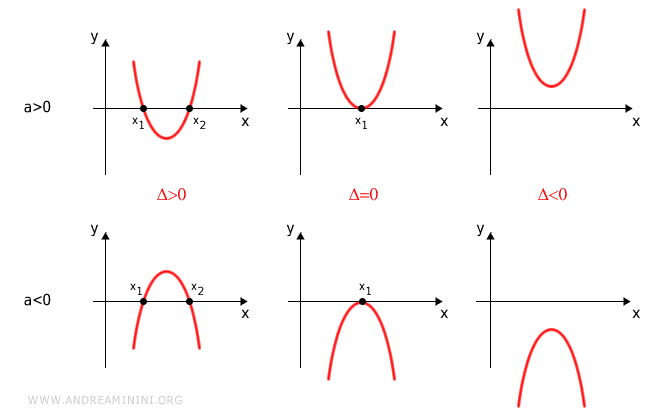
The parabola opens upward or downward depending on the sign of coefficient a: it opens upward if a>0 and downward if a<0.

A Practical Example

Let's solve the following quadratic equation:

$$ 2x^2 - 4x - 6 $$

The coefficients are a=2, b=-4, c=-6.

Using the quadratic formula:

$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

$$ x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4 \cdot 2 \cdot (-6)}}{2 \cdot 2} $$

$$ x = \frac{4 \pm \sqrt{16 + 48}}{4} $$

$$ x = \frac{4 \pm \sqrt{64}}{4} $$

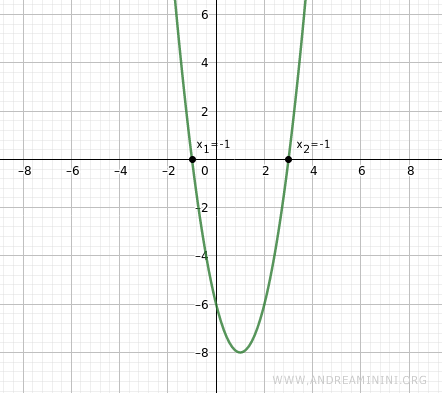
The discriminant (64) is positive (Δ>0), so the equation has two real roots.

The square root of 64 is ±8 since 8·8=64 and (-8)·(-8)=64.

$$ x = \frac{4 \pm 8}{4} $$

Simplifying:

$$ x = 1 \pm 2 $$

Thus, the roots of the equation are x₁ = -1 and x₂ = 3.

$$ x = \begin{cases} 1 - 2 = -1 \\ \\ 1 + 2 = 3 \end{cases} $$

Graphically, this equation represents an upward-opening parabola because the coefficient a>0.

Proof

To derive the quadratic formula, let’s begin with the general equation:

$$ ax^2 + bx + c = 0 $$

We apply the invariant property by multiplying both sides by 4a:

$$ 4a \cdot (ax^2 + bx + c) = 4a \cdot 0 $$

$$ 4a^2x^2 + 4abx + 4ac = 0 $$

$$ 4a^2x^2 + 4abx = -4ac $$

Next, we add and subtract \( b^2 \) on the left-hand side to form a perfect square:

$$ 4a^2x^2 + 4abx + b^2 - b^2 = -4ac $$

$$ 4a^2x^2 + 4abx + b^2 = b^2 - 4ac $$

The left-hand side is now a perfect square trinomial: \( (2ax + b)^2 \)

$$ (2ax + b)^2 = b^2 - 4ac $$

Taking the square root of both sides yields:

$$ \sqrt{(2ax + b)^2} = \sqrt{b^2 - 4ac} $$

$$ 2ax + b = \pm \sqrt{b^2 - 4ac} $$

Finally, isolating x gives the quadratic formula:

$$ 2ax = -b \pm \sqrt{b^2 - 4ac} $$

$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

Sum and Product of the Roots

If one root of a quadratic equation is already known, the other can be determined using either of the following relationships:

• Sum of the roots
  The sum of the two roots equals the negative ratio of the coefficients b and a: $$ x_1 + x_2 = -\frac{b}{a} $$
• Product of the roots
  The product of the two roots equals the ratio of the coefficients c and a: $$ x_1 \cdot x_2 = \frac{c}{a} $$

These relationships allow us to compute the missing root directly from the coefficients \(a, b, c\) of the equation \(ax^2 + bx + c = 0\), without needing to solve the equation explicitly.

Example. For the quadratic equation $$ x^2 + 4x + 3 = 0 $$ If one root is \(x_1 = -1\), we can find the other using \(a = 1\) and \(c = 3\): $$ x_2 = \frac{c}{a \cdot x_1} = \frac{3}{1 \cdot (-1)} = -3 $$ This method is particularly useful when one root is simple and easily recognizable, or when it’s already known for any reason.

Factoring a Quadratic Trinomial

A quadratic trinomial with a non-negative discriminant (\(Δ \ge 0\)) can be expressed in the equivalent factored form: $$ ax^2 + bx + c = a(x - x_1)(x - x_2) $$ where \(x_1\) and \(x_2\) are the real roots (or zeros) of the equation.

Example

Consider again the quadratic equation solved in the earlier example:

$$ 2x^2 - 4x - 6 = 0 $$

This equation has two real roots, \(x_1 = -1\) and \(x_2 = 3\).

We can therefore rewrite it in its factored form, knowing that \(a = 2\):

$$ a(x - x_1)(x - x_2) = 0 $$

$$ 2(x - (-1))(x - 3) = 0 $$

$$ 2(x + 1)(x - 3) = 0 $$

Verification. Expanding step by step: $$ 2(x + 1)(x - 3) = 0 $$ $$ (2x + 2)(x - 3) = 0 $$ $$ 2x^2 - 6x + 2x - 6 = 0 $$ $$ 2x^2 - 4x - 6 = 0 $$ The final expression matches the original quadratic equation, confirming their equivalence.

Relations Between Roots and Coefficients

For a quadratic equation in the general form \( ax^2 + bx + c = 0 \), several useful relationships link the roots \(x_1\) and \(x_2\) directly to the coefficients \(a\), \(b\), and \(c\). These relationships provide valuable insight into the equation’s structure without solving for the roots explicitly.

• Sum of the roots
  The sum of the two roots is determined by coefficient \(b\): \[ x_1 + x_2 = -\frac{b}{a} \]
• Product of the roots
  The product of the roots equals the ratio of \(c\) to \(a\): \[ x_1 \cdot x_2 = \frac{c}{a} \]
• Difference between the roots
  The difference between the roots depends on the discriminant \(\Delta = b^2 - 4ac\): \[ x_1 - x_2 = \frac{\sqrt{\Delta}}{a} \]
• Sum of the squares of the roots
  The sum of the squares of the roots is given by: \[ x_1^2 + x_2^2 = \frac{b^2 - 2ac}{a^2} \]
• Sum of the reciprocals of the roots
  The sum of the reciprocals of the roots is: \[ \frac{1}{x_1} + \frac{1}{x_2} = -\frac{b}{c} \]
• Sum of the cubes of the roots
  For the cubes of the roots: \[ x_1^3 + x_2^3 = \frac{3abc - b^3}{a^3} \]
• Sum of the squares of the reciprocals
  For the squares of the reciprocals: \[ \frac{1}{x_1^2} + \frac{1}{x_2^2} = \frac{b^2 - 2ac}{c^2} \]
• Sum of the cubes of the reciprocals
  Similarly, for the cubes of the reciprocals: \[ \frac{1}{x_1^3} + \frac{1}{x_2^3} = \frac{3abc - b^3}{c^3} \]

Example

Consider the equation \(2x^2 - 8x + 6 = 0\), where \(a = 2\), \(b = -8\), and \(c = 6\):

The sum of the roots is:

$$ x_1 + x_2 = -\frac{-8}{2} = 4 $$

The product of the roots is:

$$ x_1 \cdot x_2 = \frac{6}{2} = 3 $$

The difference between the roots, given \(\Delta = (-8)^2 - 4(2)(6) = 64 - 48 = 16\), is:

$$ x_1 - x_2 = \frac{\sqrt{16}}{2} = 2 $$

The sum of the reciprocals is:

$$ \frac{1}{x_1} + \frac{1}{x_2} = -\frac{-8}{6} = \frac{4}{3} $$

These results illustrate how powerful these relationships are: with just a few algebraic manipulations, we can describe the behavior of the roots without ever computing them directly.