System of Rational Equations
A system of equations is called a system of rational equations when at least one variable appears in the denominator of a rational expression. These systems behave like ordinary algebraic systems, but they require extra care because certain values make the expressions undefined.
How to approach a system of rational equations
When working with these systems, the key idea is to remove the fractions in a controlled way. The general procedure is straightforward:
- Identify the domain restrictions, meaning the values that make any denominator zero.
- Clear the denominators so the system becomes a set of polynomial equations.
- Solve the resulting polynomial system using your preferred method.
- Eliminate any solutions that violate the domain restrictions.
A practical example
Consider the following system. It is rational because the first equation contains fractions:
$$ \begin{cases} \frac{2}{x}+ \frac{1}{y} =0 \\ \\ 8x+15y=1 \end{cases} $$
The first step is identifying the values we must exclude. Since x and y appear in denominators, we require:
$$ C:E: \ : \ x \ne 0 \ \wedge \ y \ne 0 $$
To rewrite the system without fractions, we clear the denominators in the first equation by multiplying both sides by xy. This preserves the equation and makes the structure easier to work with.
$$ \begin{cases} xy \cdot ( \frac{2}{x}+ \frac{1}{y} ) = xy \cdot 0 \\ \\ 8x+15y=1 \end{cases} $$
$$ \begin{cases} xy \cdot \frac{2}{x} + xy \cdot \frac{1}{y} = 0 \\ \\ 8x+15y=1 \end{cases} $$
$$ \begin{cases} 2y + x = 0 \\ \\ 8x+15y=1 \end{cases} $$
At this point, we have converted the original fractional system into an equivalent polynomial one, which is simpler to handle.
Nota. Another valid approach is to use the least common denominator of the fractions. This leads to the same polynomial system. $$ \begin{cases} \frac{2y+x}{xy} =0 \\ \\ 8x+15y=1 \end{cases} $$ $$ \begin{cases} 2y+x =0 \\ \\ 8x+15y=1 \end{cases} $$
To find the solution, we use the substitution method. From the first equation, we isolate x and substitute the result into the second equation.
$$ \begin{cases} x = -2y \\ \\ 8x+15y=1 \end{cases} $$
$$ \begin{cases} x = -2y \\ \\ 8 \cdot (-2y) +15y =1 \end{cases} $$
$$ \begin{cases} x = -2y \\ \\ -16y +15y =1 \end{cases} $$
$$ \begin{cases} x = -2y \\ \\ -y =1 \end{cases} $$
$$ \begin{cases} x = -2y \\ \\ y = -1 \end{cases} $$
With y determined, we substitute y=-1 back into the first equation to find x.
$$ \begin{cases} x = -2 \cdot (-1) \\ \\ y = -1 \end{cases} $$
$$ \begin{cases} x =2 \\ \\ y =-1 \end{cases} $$
The polynomial system therefore has the solution:
$$ (x;y) = (2;-1) $$
This pair also solves the original rational system because it respects the domain restrictions.
$$ \begin{cases} x =2 \\ \\ y =-1 \\ \\ x \ne 0 \\ \\ y \ne 0 \end{cases} $$
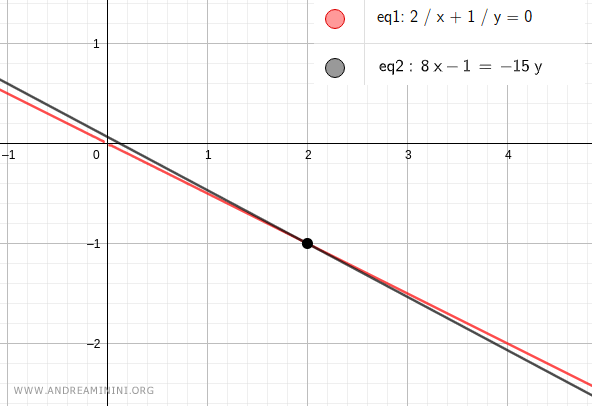
Verifica. To check the solution, we plot both equations on the Cartesian plane. The lines intersect at the point (2, -1), confirming the correctness of our result.
This approach extends naturally to more complex systems as well.
