Linear Equation

A linear equation is a first-degree equation involving one unknown $$ a \cdot x = b $$ or more than one unknown $$ a \cdot x + b \cdot y = c $$.

Linear Equations in One Variable

The solution to a linear equation in one variable, $ax = b$, is the value of $x$ that makes both sides of the equation equal.

Example. The linear equation $$ 6 = x \cdot 3 $$ has the solution $x = 2$, found by isolating $x$: $$ x = \frac{6}{3} $$ $$ x = 2 $$

Linear Equations in Two Variables

For linear equations in two variables:

$$ a \cdot x + b \cdot y = c $$

the solution consists of pairs of values $(x, y)$ that satisfy the equation.

Example. The linear equation $$ 2y + x = 6 $$ has infinitely many solutions. We can rearrange it to solve for $y$ in terms of $x$: $$ y = \frac{6 - x}{2} $$ Once we have the explicit expression for $y$, we can choose any value for $x$ and compute the corresponding value of $y$. Here are some solutions: (0, 3), (2, 2), (6, 0), and so on.

Linear equations in two variables always have infinitely many solutions, so they are called indeterminate equations.

How to Solve a First-Degree Equation

A numerical first-degree equation in the variable $x$ is an equality between two algebraic expressions in which the variable appears only to the first power. Its general form is:

$$ ax + b = cx + d $$

where $a, b, c,$ and $d$ are integers (which can be positive, negative, or zero) and $x$ is the unknown we want to solve for.

Let’s look at how to solve this kind of equation step by step.

1] Simplify and Clear Fractions

If the equation contains fractions, the first step is to eliminate denominators.

Find the least common multiple (LCM) of all denominators and multiply both sides of the equation by this value.

This results in an equation with integer coefficients only, making it simpler to solve.

Example. Consider the equation $$ \frac{2}{3}x - \frac{5}{2} = \frac{1}{6}x + 1 $$ The LCM of the denominators 3, 2, and 6 is 6. Multiply both sides by 6: $$ 6 \cdot \left(\frac{2}{3}x - \frac{5}{2}\right) = 6 \cdot \left(\frac{1}{6}x + 1\right) $$ Simplifying, we get: $$ 4x - 15 = x + 6 $$ Now the equation has only integer coefficients.

2] Gather Like Terms: Move Variables to One Side and Constants to the Other

Move all terms involving $x$ to one side of the equation and all constant terms to the other, changing their signs when you move them across the equals sign.

Then combine any like terms.

Example. Continuing from the previous equation: $$ 4x - 15 = x + 6 $$ Move $x$ to the left and $-15$ to the right: $$ 4x - x = 6 + 15 $$ Combining like terms gives: $$ 3x = 21 $$

3] Solve the Equation in the Form $ax = b$

At this stage, the equation is reduced to the form $ax = b$.

You can solve it by dividing both sides by the coefficient of $x$.

Example. Starting from: $$ 3x = 21 $$ Divide both sides by 3: $$ x = \frac{21}{3} $$ Thus, the solution is: $$ x = 7 $$

4] Check the Solution

Once you find a solution, it’s good practice to substitute it back into the original equation to verify that it satisfies the equation.

Example. Substitute $x = 7$ into the original equation: $$ \frac{2}{3} \cdot 7 - \frac{5}{2} = \frac{1}{6} \cdot 7 + 1 $$ Calculate both sides: $$ \frac{14}{3} - \frac{5}{2} = \frac{7}{6} + 1 $$ Converting to decimals for simplicity: $$
4.\overline{6} - 2.5 = 1.16\overline{6} + 1 $$ $$ 2.16\overline{6} = 2.16\overline{6} $$ The solution checks out.

By following these steps, you can solve any numerical first-degree equation in one variable.

Determinate, Indeterminate, and Impossible Equations

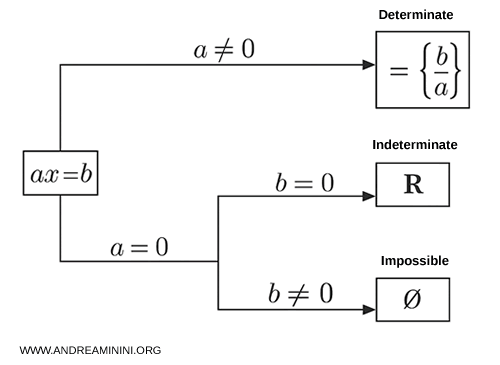
A first-degree equation is said to be determinate when it has exactly one real solution.

In these cases, the variable’s coefficient is nonzero, which means we can solve the equation simply by dividing both sides by that coefficient.

For example, consider the following first-degree equation: $$ 2x = 10 $$ Here, $ a = 2 $ and $ b = 10 $. Dividing both sides by 2 gives: $$ x = \frac{10}{2} = 5 $$ So the equation has a unique solution, $ x = 5 $.

An equation is called indeterminate (or an identity) if it’s true for every real number $ x $.

This happens, for instance, when the variable term is multiplied by zero ($ a = 0 $) and the other side of the equation is also zero ($ b = 0 $).

For example, this equation is an identity: $$ 0 \cdot x = 0 $$ Any real number multiplied by zero equals zero, so every real number is a solution. Therefore, the solution set is $\mathbb{R}$.

An equation is considered impossible when there’s no value of $ x $ that makes it true.

This happens, for example, when the variable is multiplied by zero ($ a = 0 $), but the other side of the equation is not zero ($ b \ne 0 $), resulting in $ 0 \cdot x = b $.

For instance, the following equation is impossible: $$ 0 \cdot x = 5 $$ No number multiplied by zero can ever equal 5. So the equation has no solution, and its solution set is empty: $\varnothing$.

And so on.