Pencil of Planes

A pencil of planes is an infinite collection of planes defined by a real parameter. Depending on the context, the planes may either share a common line of intersection or be parallel throughout.

Proper pencil of planes

Given a line r, a proper pencil of planes consists of all planes that contain the line r. $$ \lambda_1 ( a_1x+b_1y+c_1z+d_1 ) + \lambda_2 ( a_2x+b_2y+c_2z+d_2 ) = 0 $$ $$ ( a_1x+b_1y+c_1z+d_1 ) + \frac{\lambda_2}{\lambda_1} ( a_2x+b_2y+c_2z+d_2 ) = 0 $$

These two equations define two distinct planes.

Their intersection is the line r.

$$ \begin{cases} \lambda_1 ( a_1x+b_1y+c_1z+d_1 ) \\ \lambda_2 ( a_2x+b_2y+c_2z+d_2 ) \end{cases} $$

Example

Suppose we are given the equation of a line in space, defined by the intersection of two planes:

$$ \begin{cases} 2x+3y+8z+2=0 \\ -4x-6y+6z-12=0 \end{cases} $$

The set of points lying at the intersection of these two planes forms the line.

In this case, the proper pencil of planes passing through the line is expressed as:

$$ ( 2x+3y+8z+2 ) + \frac{\lambda_2}{\lambda_1} ( -4x-6y+6z-12 ) = 0 $$

where \(\lambda_1\) and \(\lambda_2\) are arbitrary scalars, with \(\lambda_2 \neq 0\).

For simplicity, we can write \( k = \lambda_2 / \lambda_1 \), so the equation becomes:

$$ ( 2x+3y+8z+2 ) + k ( -4x-6y+6z-12 ) = 0 $$

By varying \( k \), we obtain all planes in the pencil that contain the line r - that is, all planes "rotating" about the line.

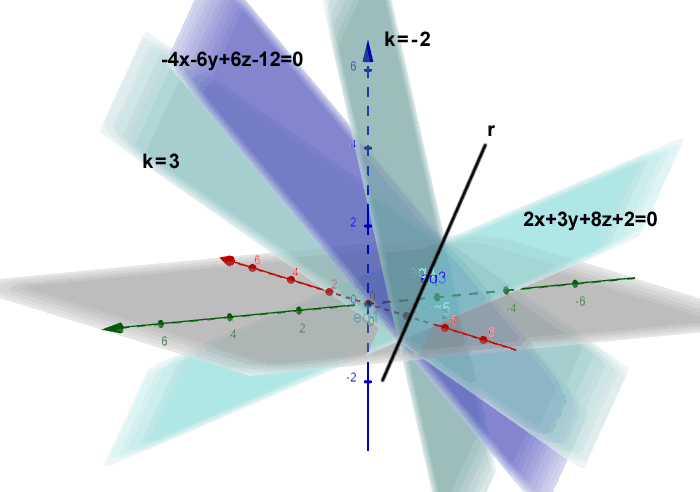
This is the proper pencil of planes associated with the line r.

 

Improper pencil of planes

Given a plane A, an improper pencil of planes consists of all planes parallel to A. $$ ax+by+cz+d=0 $$

To generate the parallel planes, simply vary the constant term \( d \).

The coefficients \( a, b, c \) must not all be zero at the same time.

Example

Consider the equation of a plane in space:

$$ 2x+3y+8z+2=0 $$

By varying the constant term \( k \), we obtain the family of planes parallel to the given plane:

$$ 2x+3y+8z+k=0 $$

For instance, with \( k = -12 \) and \( k = -25 \), the graphical representation is as follows:

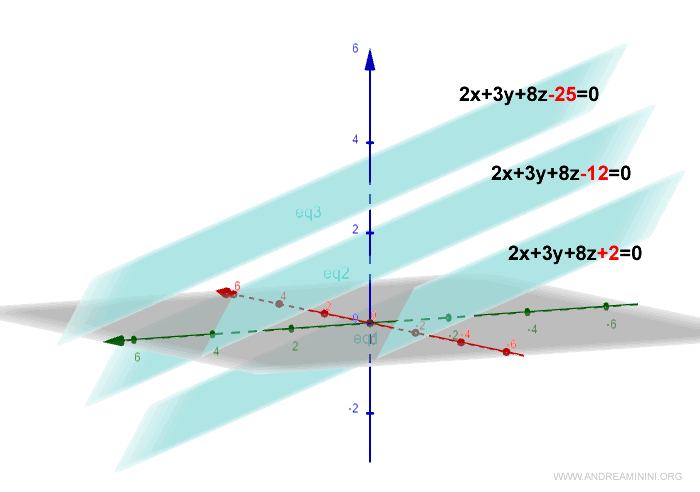
And so on.