The Vector Space of Applied Geometric Vectors

The vector space of geometric vectors in a plane applied to point O is a collection of vectors originating at point O and extending to any other point in the plane.

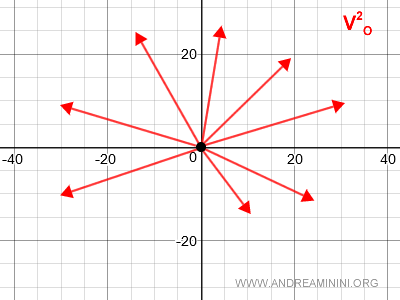
a practical example

Explanation

Given a point O in a plane, the set of vectors applied at O forms a vector space V²_O.

What is a vector applied at O? It's a vector OP that starts at O and ends at point P.
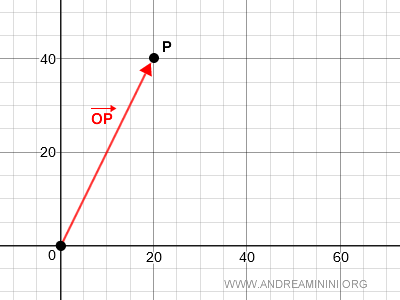
an example of an applied vector

In the vector space V²_O, operations like vector addition and scalar multiplication can be performed.

Vector Addition

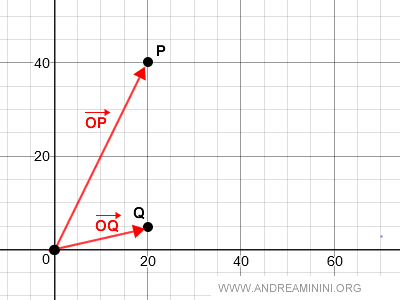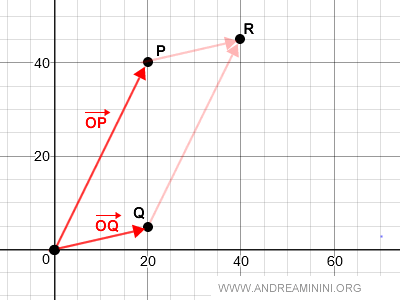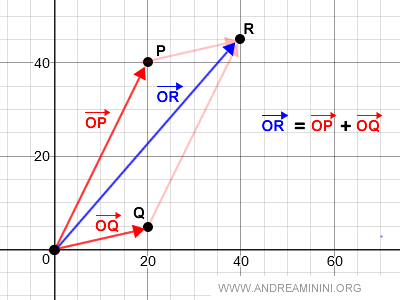
Given two vectors OP and OQ, their addition is as follows:

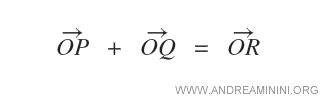
the sum of geometric vectors OP+OQ=OR

Following the parallelogram rule, the addition of vectors is the diagonal of the parallelogram OPRQ.

Graphically, the addition of two geometric vectors is as follows:

the addition of two geometric vectors using the parallelogram method

Scalar Multiplication of a Vector

Given a vector OP and a scalar α, the result of their multiplication is a new vector OQ, which starts at point O and ends at point Q.

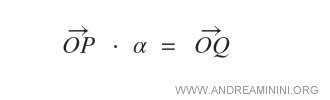
the scalar product of vector OQ = α OP

The slope of vector OQ is calculated as follows:

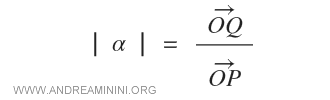
the angular coefficient of vector OQ obtained by scalar multiplication |α|=OQ/OP

Here’s how scalar multiplication of a vector is represented in two dimensions:

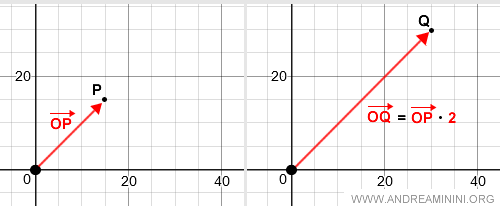
the graphical representation of the scalar product

Depending on whether α is positive or negative, vector OQ will point in the same direction as OP or in the opposite direction.

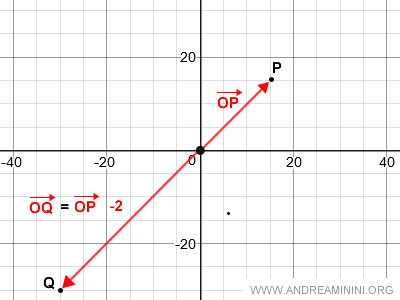
the scalar product of the opposite vector

The direction of vectors OQ and OP is always aligned, as the absolute value of the slope |α| remains the same.

Special Cases

If the scalar α is one (α=1), the resulting vector OQ is identical to vector OP.

If the scalar α is negative one (α=-1), the resulting vector OQ is the opposite vector OP', where point P' is the mirror image of P across O.

If the scalar α is zero (α=0), the product of OP with the scalar is the point OO, resulting in a null vector OO.