Dependent Linear Systems

A system of equations is dependent when its equations describe the same relationship, so the system has infinitely many solutions.

In particular, consider a first degree linear system written in standard form

$$ \begin{cases} a_1x + b_1y = c_1 \\ \\ a_2x + b_2y = c_2 \end{cases} $$

A system has infinitely many solutions when the ratios of the coefficients of x and y match the ratio of the constant terms

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} $$

This provides a quick way to recognize a dependent linear system, that is, a system with infinitely many solutions, without carrying out a full algebraic solution.

Note. If the ratios a₁/a₂ and b₁/b₂ both equal c₁/c₂, then the two equations define the same line. They have identical slopes and identical y intercepts. Because coincident lines represent the same set of points, the system has infinitely many solutions.

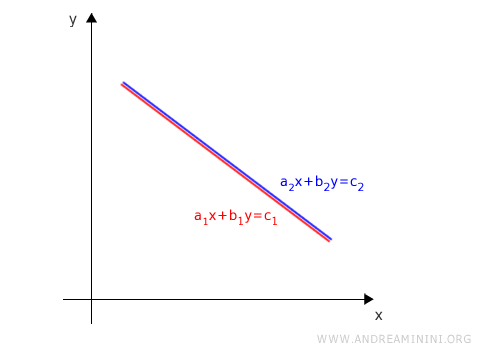
This happens precisely when the equations are equivalent, meaning one is a scalar multiple of the other.

A practical example

Let us determine whether the system below has infinitely many solutions

$$ \begin{cases} 2x + 4y = 3 \\ \\ 4x + 8y = 6 \end{cases} $$

The first step is to compare the ratios of the coefficients of x and y

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} $$

Here a₁=2, b₁=4, a₂=4, b₂=-8

$$ \frac{2}{4} = \frac{4}{8} $$

$$ \frac{1}{2} = \frac{1}{2} $$

The first condition holds: the ratios of the corresponding coefficients coincide.

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{1}{2} $$

This tells us that the two lines have the same slope.

Note. If the ratios had been different, the system would consist of two lines with distinct slopes, which intersect in exactly one point. In that case the system would be a consistent system, and checking the second condition would serve no purpose.

We now check whether the ratio of the coefficients also matches the ratio of the constant terms.

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} $$

We already know that a₁/a₂ and b₁/b₂ both equal 1/2

$$ \frac{1}{2} = \frac{c_1}{c_2} $$

Since c₁=3 and c₂=6

$$ \frac{1}{2} = \frac{3}{6} $$

$$ \frac{1}{2} = \frac{1}{2} $$

The second condition is also satisfied.

Thus, the system has infinitely many solutions and is therefore dependent.

Verification. A graphical check confirms this. Plotting both equations shows that they coincide, so they share infinitely many points. This matches the algebraic result.

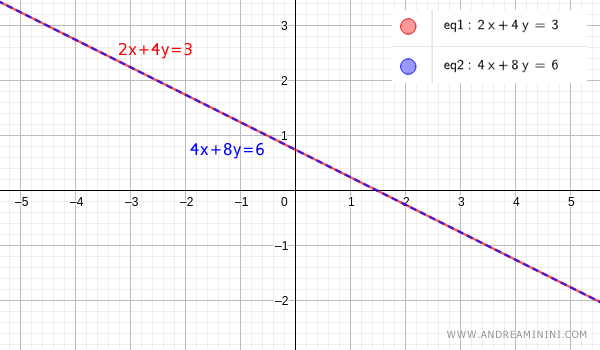
Example 2

The same system can be recognized even more quickly

$$ \begin{cases} 2x + 4y = 3 \\ \\ 4x + 8y = 6 \end{cases} $$

At a glance, each coefficient in the first equation is half of the corresponding coefficient in the second

$$ \begin{cases} \color{red}2x + \color{blue}4y = \color{green}3 \\ \\ \color{red}4x + \color{blue}8y = \color{green}6 \end{cases} $$

Applying the invariance property and multiplying both sides of the first equation by 2

$$ \begin{cases} 2 \cdot( 2x + 4y ) = 2 \cdot 3 \\ \\ 4x + 8y = 6 \end{cases} $$

$$ \begin{cases} 4x + 8y = 6 \\ \\ 4x + 8y = 6 \end{cases} $$

The equations now coincide exactly. They describe the same line and therefore the system has infinitely many solutions.

The proof

Consider a first degree linear system in two variables x and y

$$ \begin{cases} a_1x + b_1y = c_1 \\ \\ a_2x + b_2y = c_2 \end{cases} $$

We rewrite each equation in slope intercept form

$$ \begin{cases} y = -\frac{a_1}{b_1} x + \frac{c_1}{b_1} \\ \\ y = -\frac{a_2}{b_2} x + \frac{c_2}{b_2} \end{cases} $$

Plotted on the Cartesian plane, each equation corresponds to a straight line.

Each line represents the solution set of one linear equation in the system.

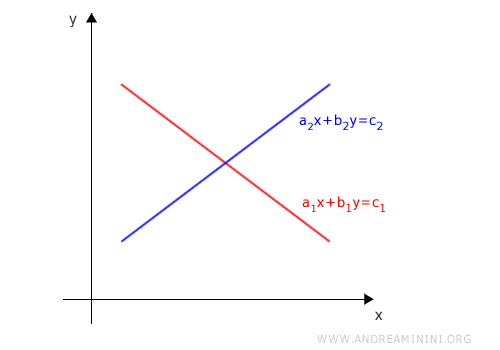
If two lines have different slopes, they intersect in exactly one point.

In this case, the system has a unique solution and is a consistent system.

To avoid a single point of intersection, the lines must have the same slope.

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} $$

Note. The equality of slopes can be expressed in several equivalent ways. For instance, $$ - \frac{a_1}{b_1} = - \frac{a_2}{b_2} $$ Multiplying both sides by -1 yields $$ \frac{a_1}{b_1} = \frac{a_2}{b_2} $$ Multiplying by b₁/a₂ and simplifying, we obtain $$ \frac{a_1}{a_2} = \frac{b_1}{b_2} $$ Many textbooks rewrite this in algebraic form as $$ a_1 b_2 = a_2 b_1 $$ or $$ a_1 b_2 - a_2 b_1 = 0 $$ The geometric meaning is the same.

However, equal slopes alone do not guarantee infinitely many solutions.

Lines with the same slope may still be parallel.

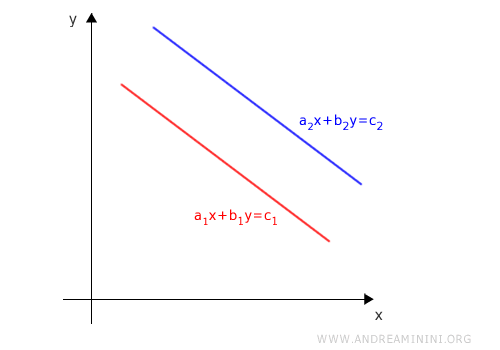
Note. Parallel lines never meet, so the system has no solutions and is an inconsistent system.

To avoid parallelism, the lines must also share the same y intercept.

The y intercepts are given by c₁/b₁ and c₂/b2

$$ \begin{cases} y = -\frac{a_1}{b_1} x \color{red}{ + \frac{c_1}{b_1} } \\ \\ y = -\frac{a_2}{b_2} x \color{red} {+ \frac{c_2}{b_2} } \end{cases} $$

Equating these intercepts gives

$$ \frac{c_1}{b_1} = \frac{c_2}{b_2} $$

A simple algebraic rearrangement yields

$$ \frac{c_1}{c_2} = \frac{b_1}{b_2} $$

Since b₁/b₂ equals a₁/a₂ whenever the slopes match

$$ \frac{c_1}{c_2} = \frac{b_1}{b_2} = \frac{a_1}{a_2} $$

Thus, in order for two lines with the same slope not to be parallel, the ratio of the coefficients a₁/a₂ = b₁/b₂ must match the ratio of the constants c₁/c₂.

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} $$

When this condition holds, the lines coincide.

Coincident lines share infinitely many points, so the system has infinitely many solutions. It is a dependent system.

This completes the proof.

And so on.