Linear Systems with a Unique Solution

A system of equations has a unique solution when it admits exactly one solution, that is, when the two equations intersect in a single point.

In particular, a first degree linear system

$$ \begin{cases} a_1x + b_1y = c_1 \\ \\ a_2x + b_2y = c_2 \end{cases} $$

has a unique solution when the ratios of the coefficients of x and y in the two equations are different

$$ \frac{a_1}{a_2} \ne \frac{b_1}{b_2} $$

This provides a quick and effective criterion for determining whether a linear system admits exactly one solution.

Note. If a₁/a₂ equals b₁/b₂, then the two lines have the same slope, since a₁/b₁ = a₂/b₂. In that case the lines are either parallel, with no points in common, or coincident, sharing infinitely many points. In both situations the system does not have a unique solution.

A practical example

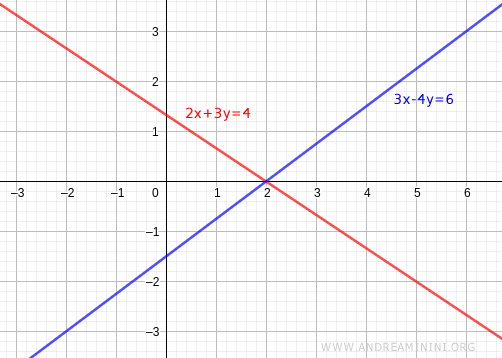
We want to determine whether the following linear system has a unique solution

$$ \begin{cases} 2x + 3y = 4 \\ \\ 3x - 4y = 6 \end{cases} $$

We compare the ratios of the corresponding coefficients

$$ \frac{a_1}{a_2} \ne \frac{b_1}{b_2} $$

The coefficients are a₁ = 2, b₁ = 3, a₂ = 3 and b₂ = -4

$$ \frac{2}{3} \ne \frac{3}{-4} $$

Since the ratios differ,

the system admits a unique solution.

Verification. A graphical check confirms this. The two lines meet at the point P(2,0). Since there is exactly one intersection point, the system has a unique solution.

The reasoning behind the criterion

A first degree linear system in two variables can always be represented in the Cartesian plane.

$$ \begin{cases} a_1x + b_1y = c_1 \\ \\ a_2x + b_2y = c_2 \end{cases} $$

Each linear equation corresponds to a straight line.

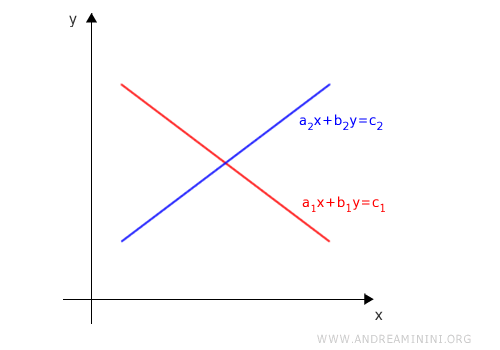
Note. A point lies on a line exactly when its coordinates (x,y) satisfy the equation.

Geometrically, the solution of the system is the intersection point of the two lines.

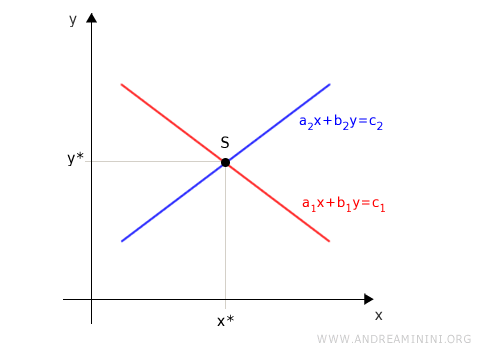
At the intersection point S(x,y) both equations hold simultaneously.

Therefore, a linear system in two variables admits a unique solution only when the two lines have different slopes.

Explanation. If the slopes coincide, the system cannot have a unique solution, because the lines are either parallel or coincident. Parallel lines do not intersect, so the system has no solutions and is inconsistent.

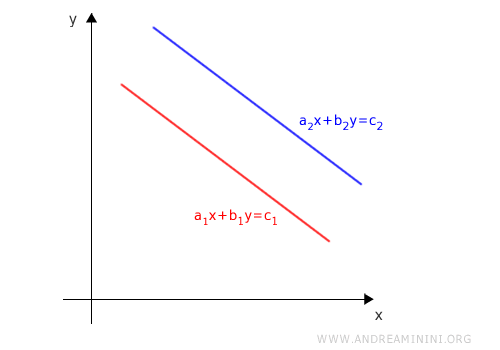
If the lines coincide, they share infinitely many points and the system is dependent.

We now rewrite the system in explicit form

$$ \begin{cases} y = -\frac{a_1}{b_1} x + \frac{c_1}{b_1} \\ \\ y = -\frac{a_2}{b_2} x + \frac{c_2}{b_2} \end{cases} $$

The slopes are different precisely when -a₁/b₁ differs from -a₂/b₂

$$ -\frac{a_1}{b_1} \ne -\frac{a_2}{b_2} $$

Multiplying both sides by -1

$$ \frac{a_1}{b_1} \ne \frac{a_2}{b_2} $$

Then multiplying both sides by b₁/a₂ and simplifying

$$ \frac{a_1}{a_2} \ne \frac{b_1}{b_2} $$

This shows that when the slopes differ, the ratios of the coefficients of x and y must also differ

$$ \frac{a_1}{a_2} \ne \frac{b_1}{b_2} $$

which is exactly what we set out to prove.

Note. In university textbooks the same condition is often expressed in equivalent algebraic forms such as $$ a_1 b_2 \ne a_2 b_1 $$ or $$ a_1 b_2 - a_2 b_1 \ne 0 $$. Geometrically they all express the same idea.