Inconsistent Linear System

A system of equations is inconsistent when it has no solution.

Consider a linear system in two unknowns, x and y:

$$ \begin{cases} a_1x + b_1y = c_1 \\ \\ a_2x + b_2y = c_2 \end{cases} $$

The system is inconsistent precisely when the following two conditions hold:

• the ratios of the coefficients of x and y are equal $$ \frac{a_1}{a_2} = \frac{b_1}{b_2} $$
• but this common ratio differs from the ratio of the constant terms $$ \frac{a_1}{a_2} = \frac{b_1}{b_2} \ne \frac{c_1}{c_2} $$

This provides an immediate and fully general criterion for identifying linear systems with no solution, without performing further algebraic manipulations.

Note. If the ratios a₁/a₂ and b₁/b₂ differ, then the slopes of the two lines, -a₁/b₁ and -a₂/b₂, are different. Lines with distinct slopes intersect in exactly one point, so the system has a unique solution and is a consistent independent system. If instead a₁/a₂ = b₁/b₂ and this value also equals c₁/c₂, the two equations represent the same line. In that case the system is consistent dependent and admits infinitely many solutions.

A Practical Example

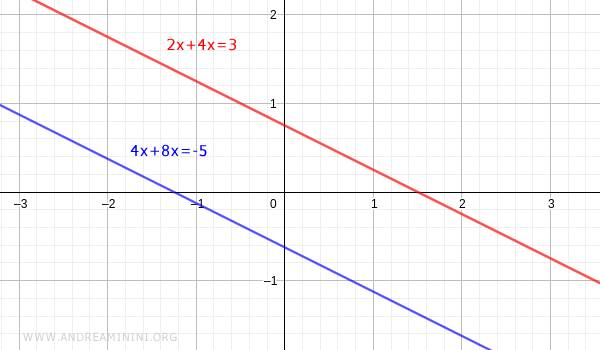
Let me determine whether the following linear system is consistent:

$$ \begin{cases} 2x + 4y = 3 \\ \\ 4x + 8y = -5 \end{cases} $$

I first check whether the coefficient ratios coincide:

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} $$

Here a₁=2, b₁=4, a₂=4, b₂=-8

$$ \frac{2}{4} = \frac{4}{8} $$

$$ \frac{1}{2} = \frac{1}{2} $$

The ratios match.

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{1}{2} $$

The first condition is satisfied.

Note. Had the ratios been unequal, the system would already be known to have a unique solution and no further checks would be necessary.

To determine whether the system is inconsistent, I compare this ratio with the ratio of the constant terms:

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} \ne \frac{c_1}{c_2} $$

Since the coefficient ratio is 1/2,

$$ \frac{1}{2} \ne \frac{c_1}{c_2} $$

and the constants are c₁=3 and c₂=-5,

$$ \frac{1}{2} \ne -\frac{3}{5} $$

The second condition is satisfied.

The system is therefore inconsistent and admits no solution.

Verification. The graphical representation confirms this: the two lines are parallel and do not intersect, so there is no point that simultaneously satisfies both equations.

Proof

Consider again a linear system in two variables:

$$ \begin{cases} a_1x + b_1y = c_1 \\ \\ a_2x + b_2y = c_2 \end{cases} $$

A linear system in two variables can be represented geometrically in the Cartesian plane. Each linear equation corresponds to a straight line.

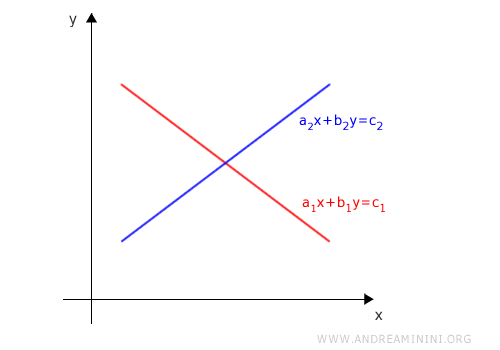
Note. Every point on the graph of an equation is an ordered pair (x, y) that satisfies that equation.

If the two lines intersect in a single point, the system has exactly one solution (a consistent independent system).

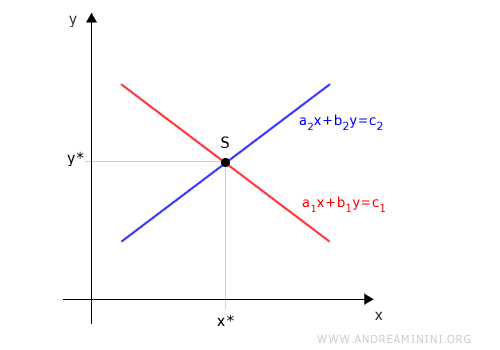
A system is inconsistent only when the corresponding lines do not meet.

This occurs precisely when the lines are parallel and distinct.

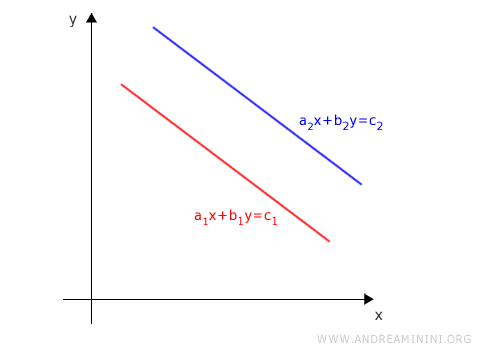
Two lines are parallel when they have the same slope but different y-intercepts.

Writing the system in slope intercept form yields:

$$ \begin{cases} y = -\frac{a_1}{b_1} x + \frac{c_1}{b_1} \\ \\ y = -\frac{a_2}{b_2} x + \frac{c_2}{b_2} \end{cases} $$

Parallelism requires that the slopes be identical:

$$ -\frac{a_1}{b_1} = -\frac{a_2}{b_2} $$

Multiplying both sides by -1 gives:

$$ \frac{a_1}{b_1} = \frac{a_2}{b_2} $$

Multiplying by b₁/a₂ and simplifying leads to:

$$ \frac{a_1}{b_1} \cdot \left( \frac{b_1}{a_2} \right) = \frac{a_2}{b_2} \cdot \left( \frac{b_1}{a_2} \right) $$

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} $$

Note. Textbooks often present equivalent algebraic forms, such as $$ a_1 b_2 = a_2 b_1 $$ or $$ a_1 b_2 - a_2 b_1 = 0 $$ all of which express the same geometric condition.

Equal slopes alone are not enough to guarantee distinct parallel lines.

If the slopes and intercepts are both equal, the lines coincide.

Coincident lines have infinitely many points in common, yielding a system with infinitely many solutions (a consistent dependent system).

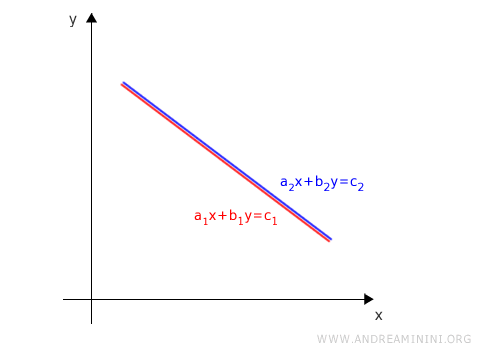
To ensure that the lines are distinct, the coefficient ratio a₁/a₂ = b₁/b₂ must differ from the ratio c₁/c₂.

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} \ne \frac{c_1}{c_2} $$

Under this condition the lines are parallel, distinct, and share no points, so the system is inconsistent.

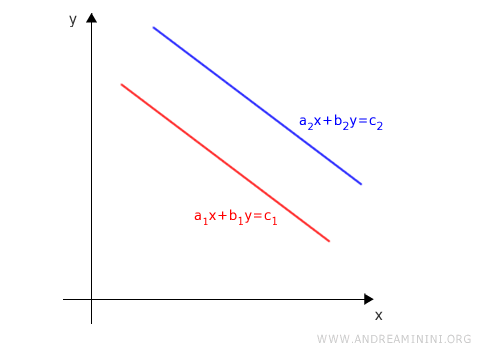
This completes the argument.

And so on.