Exercises on Vector Spaces

Here are some worked examples on vector spaces.

Exercise 1

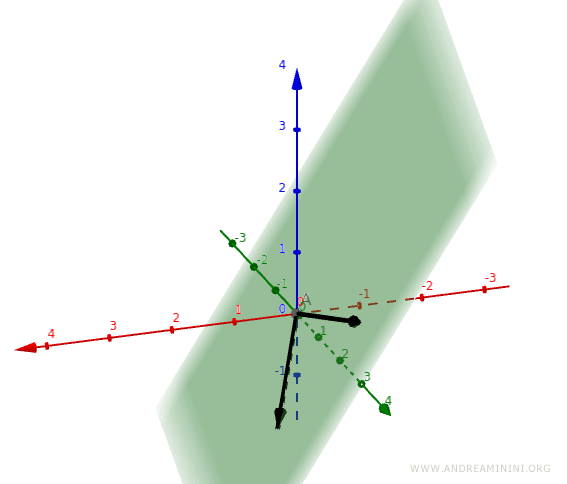
Consider the following two vectors in the vector space V = R³:

$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} 0 \\ 3 \\ 1 \end{pmatrix} $$

Do these two vectors span R³?

To answer this, we need to determine whether an arbitrary vector v in R³:

$$ v = \begin{pmatrix} a \\ b \\ c \end{pmatrix} \ \in V = R^3 $$

can be written as a linear combination of v₁ and v₂:

$$ \vec{v} = \lambda_1 \cdot \vec{v}_1 + \lambda_2 \cdot \vec{v}_2 $$

$$ \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \lambda_1 \cdot \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 0 \\ 3 \\ 1 \end{pmatrix} $$

This leads to a system of three equations in two unknowns:

$$ \begin{cases} \lambda_1 = a \\ 2 \lambda_1 + 3 \lambda_2 = b \\ - \lambda_1 + \lambda_2 = c \end{cases} $$

Substituting λ₁ = a into the other two equations, we obtain:

$$ \begin{cases} \lambda_1 = a \\ 2 a + 3 \lambda_2 = b \\ \lambda_2 = c + a \end{cases} $$

Substituting λ₂ = c + a into the second equation gives:

$$ 2 a + 3 (c + a) = b $$

which simplifies to:

$$ 5 a + 3 c = b $$

This shows that the system has solutions only if this condition is satisfied. In other words, the system does not have solutions for arbitrary values of a, b, and c.

Therefore, the two vectors v₁ and v₂ do not span the entire vector space V = R³.

Note. In general, two linearly independent vectors can span at most a plane (R²) in the space they inhabit. Since V = R³ is three-dimensional, at least three linearly independent vectors would be required to span the entire space.

Exercise 2

Consider the vector space M(2,2,R), the set of all 2x2 real matrices. Is the subset A of M(2,2,R), consisting of matrices of the form: $$ \begin{pmatrix} a & b \\ c & 1 \end{pmatrix} \ \ \ \ a,b,c \in R $$ a vector subspace of M(2,2,R)?

To answer this, we check whether A satisfies the axioms of a vector space and the conditions for being a subspace.

1] Is subset A a vector space?

The set A is clearly non-empty.

However, it is immediately obvious that the zero matrix (the additive identity):

$$ \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \ \ \notin \ A $$

is not an element of A. The presence of the zero matrix is a necessary condition for a set to form a vector space.

Therefore, A is not a vector space, and thus A is not a subspace of M(2,2,R).

Note. This example highlights the value of first checking the simplest conditions - such as the presence of the additive identity - before moving on to the more involved ones. This saves both time and effort.

Exercise 3

Consider the vector space M(2,2,R), the set of all 2x2 real matrices. Is the subset A of M(2,2,R), consisting of matrices of the form: $$ \begin{pmatrix} a & b \\ c & b-1 \end{pmatrix} \ \ \ \ a,b,c \in R $$ a subspace of M(2,2,R)?

We first check whether A satisfies the axioms of a vector space.

Then we verify whether it meets the conditions for a subspace.

1] Is subset A a vector space?

Subset A is clearly non-empty.

However, it is immediately apparent that the zero matrix is not an element of A:

$$ \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \ \ \notin \ A $$

The reason is that two elements in the matrix depend on the same parameter, specifically b and b-1:

$$ \begin{pmatrix} a & \color{red}b \\ c & \color{red}{b-1} \end{pmatrix} \ \ \ \ a,b,c \in R $$

For example, choosing a = 0, b = 0, c = 0 yields:

$$ \begin{pmatrix} 0 & 0 \\ 0 & \color{red}{-1} \end{pmatrix} \ \ \ \ a,b,c \in R $$

Similarly, setting a = 0, b = 1, c = 0 gives:

$$ \begin{pmatrix} 0 & \color{red}{1} \\ 0 & 0 \end{pmatrix} \ \ \ \ a,b,c \in R $$

Since the additive identity is required for a vector space, we can conclude that A is not a vector space.

Therefore, A cannot be a subspace of M(2,2,R).

And so on.