Cramer's Method for Rectangular Systems

A familiar limitation of Cramer's Theorem is that it applies only to square linear systems. This sharply restricts its direct use. Even so, the method can still be leveraged when a rectangular system is reworked into a suitable square subsystem.

If a rectangular system can be reduced to an equivalent square subsystem, then Cramer's Method can be applied to compute its solutions.

For example, a 3x4 system can be handled via Cramer's Method if it can be reduced to a 3x3 or 2x2 subsystem.

Reducing a rectangular system to a square one

To convert a rectangular system into a square one, we remove redundant equations and identify the free variables that span the solution space.

The reduction procedure

Given the matrix M associated with a nonzero minor of maximal order, which determines the rank r of both the coefficient matrix A and the augmented matrix A|B:
1. we discard the equations corresponding to the rows of A not represented in M.
2. we treat as free parameters the unknowns associated with the columns of A not appearing in M.

A worked example

The system below is rectangular, with three equations and four unknowns.

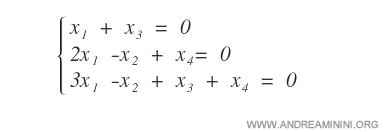
We first express the system in matrix form.

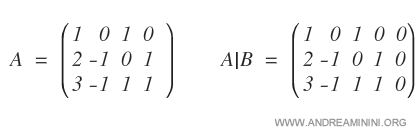
Cramer's Method cannot be used directly because the coefficient matrix A is 3x4 and therefore non square.

How do we obtain a square subsystem?

Before proceeding, we must check that the system is consistent.

We compute appropriate minors of both A and A|B to determine their rank.

We select the last two rows and the third and fourth columns to form the submatrix A_(2,3)(3,4).

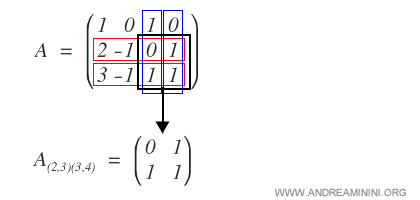
We then compute the determinant of this submatrix, that is, the relevant minor.

Because the minor of A_(2,3)(3,4) is nonzero, A has rank at least 2.

To determine whether the rank is higher, we apply the Bordering Theorem to A_(2,3)(3,4).

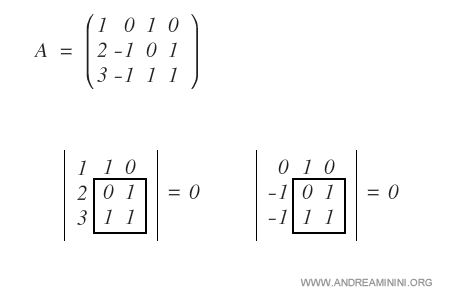
No bordered matrix of order three produces a nonzero determinant, so the matrix does not have rank three.

Thus, the rank of A is exactly 2.

$$ rg(A)=2 $$

We now examine the rank of the augmented matrix A|B.

Since all constant terms are zero, it is immediate that A|B also has rank 2.

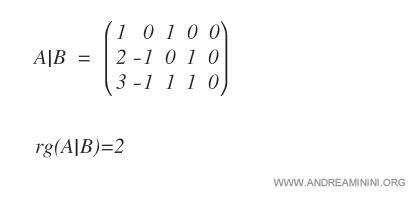
By the Rouché Capelli Theorem, the system is consistent because the ranks of A and A|B coincide.

With four unknowns (n = 4) and rank 2 (r = 2), the solution set is infinite dimensional. In other words, the system has infinitely many solutions.

$$ \infty^{n-r} = \infty^{4-2} = \infty^2 = \infty \ solutions $$

Having ensured consistency, we now reduce A to a square subsystem.

1] Remove the first row of the matrix, since it does not affect the solution set.

The corresponding equation is discarded because it does not appear in the maximal minor A_(2,3)(3,4).

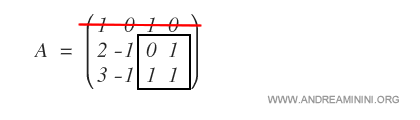
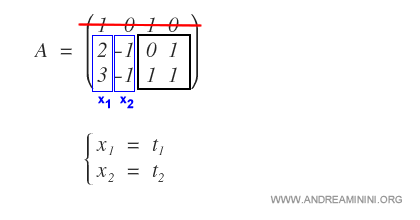
2] Introduce parameters t₁ and t₂ for the first two columns.

The first two columns correspond to x₁ and x₂, which do not appear in the maximal minor and therefore function as free variables.

After these steps, the system can be rewritten in the following form:

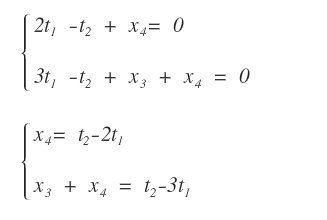
In this parametrized version, the system has a square coefficient matrix.

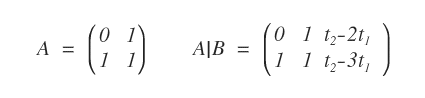
We can now apply Cramer's Theorem to compute the remaining unknowns.

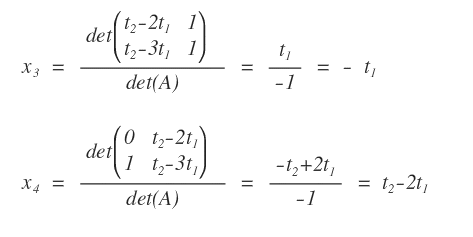
This yields explicit expressions for x₃ and x₄.

Note. The variables x₁ and x₂ are not computed explicitly because they serve as parameters.

The complete solution set can now be written.

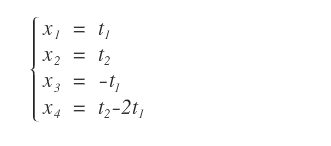
In summary, this approach allows us to use Cramer's Theorem to solve a rectangular system by isolating a square subsystem and parametrizing the remaining variables.

Warning. The choice of which variables to parametrize depends on the initial minor selected. The resulting parametric form of the solution therefore reflects this choice. The method is not fully canonical. Certain parametrizations lead to cleaner and more transparent solutions than others.