Comparison Test for Improper Integrals

If the improper integral of $ g(x) $ converges, then the improper integral of $ f(x) $ also converges.
If the improper integral of $ f(x) $ diverges, then the improper integral of $ g(x) $ must diverge as well.

Proof and Explanation
A Practical Example

Proof and Explanation

Assume $ f(x) $ and $ g(x) $ are defined over the interval $[a, b]$.

$$ f(x) \le g(x) $$

Then, by the comparison property of definite integrals:

$$ \int_a^b f(x) \:dx \le \int_a^b g(x) \: dx $$

Case 1

If the limit of the second integral exists as $ b \to \infty $ and equals a finite number $ l $, that is, the integral of $ g(x) $ converges,

$$ l = \lim_{b \rightarrow \infty} \int_a^b g(x) \: dx $$

then the first limit must be less than or equal to $ l $:

$$ \lim_{b \rightarrow \infty} \int_a^b f(x) \: dx \le l $$

Therefore, the integral of $ f(x) $ also converges.

Case 2

If the limit of the first integral is infinite - meaning that the integral of $ f(x) $ diverges - then, since $ g(x) \ge f(x) $, the second integral must also diverge:

$$ \lim_{b \rightarrow \infty} \int_a^b f(x) \: dx = \infty $$

implies

$$ \lim_{b \rightarrow \infty} \int_a^b g(x) \: dx \ge \infty $$

and hence:

$$ \lim_{b \rightarrow \infty} \int_a^b g(x) \: dx = \infty $$

A Practical Example

Let’s determine whether the improper integral of the function $ f(x) = e^{-x^2} $ converges over the interval $[0, \infty)$:

$$ \int_0^{\infty} e^{-x^2} \: dx $$

Note: Computing the limit directly is not straightforward: $$ \int_0^{\infty} e^{-x^2} \: dx = \lim_{b \rightarrow +\infty } \int_0^b e^{-x^2} \: dx $$ because the antiderivative of $ e^{-x^2} $ is not expressible in terms of elementary functions.

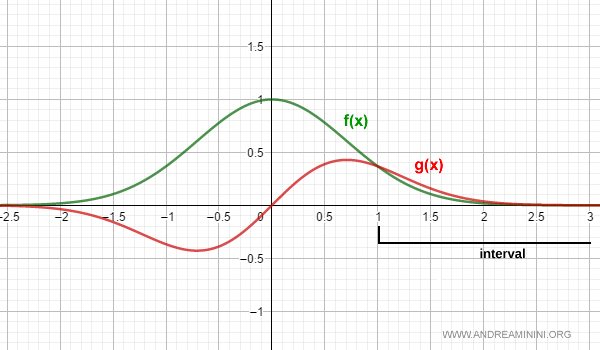
To simplify the analysis, let’s restrict the domain to the interval $[1, \infty)$, and compare $ f(x) $ with the function $ g(x) = e^{-x^2} \cdot x $:

$$ \int_1^{\infty} e^{-x^2} \cdot x \: dx $$

On this interval, it holds that:

$$ e^{-x^2} \le e^{-x^2} \cdot x $$

Therefore, by the comparison test:

$$ \int_1^{\infty} e^{-x^2} \: dx \le \int_1^{\infty} e^{-x^2} \cdot x \: dx $$

The second integral is more approachable, since its antiderivative is elementary:

$$ \int_1^{\infty} e^{-x^2} \cdot x \: dx = \lim_{ b \rightarrow \infty } \int_1^b e^{-x^2} \cdot x \: dx $$

$$ = \lim_{ b \rightarrow \infty } \left[ - \frac{1}{2} e^{-x^2} \right]_1^b $$

$$ = \lim_{ b \rightarrow \infty } - \frac{1}{2} e^{-b^2} + \frac{1}{2} e^{-1} $$

$$ = \lim_{ b \rightarrow \infty } - \frac{1}{2} e^{-b^2} + \frac{1}{2e} $$

$$ = 0 + \frac{1}{2e} $$

$$ = \frac{1}{2e} $$

Thus, the improper integral of $ g(x) $ converges to $ \frac{1}{2e} $:

$$ \int_1^{\infty} e^{-x^2} \cdot x \: dx = \frac{1}{2e} $$

And since:

$$ \int_1^{\infty} e^{-x^2} \: dx \le \int_1^{\infty} e^{-x^2} \cdot x \: dx $$

$$ \int_1^{\infty} e^{-x^2} \: dx \le \frac{1}{2e} $$

we can conclude that the improper integral of $ f(x) $ also converges.

graph illustrating the comparison test for improper integrals

And so on.