Antiderivatives
What is an antiderivative?
A function F(x) is an antiderivative of a function f(x) if F(x) is differentiable on the interval [a, b] and its derivative satisfies $$ F'(x) = f(x) \quad \text{for all } x \in [a, b] $$
A practical example
Take the function:
$$ F(x) = x^2 $$
This is an antiderivative of f(x) = 2x
$$ f(x) = 2x $$
because its derivative matches f(x):
$$ F'(x) = D[x^2] = 2x $$
This observation underpins the Fundamental Theorem of Calculus.
If f(x) is continuous on [a, b], then a function F(x) is an antiderivative of f(x) if its derivative equals f(x): $$ F(x) = \int_a^b f(x) \: dx $$ with $$ f(x) = F'(x) $$
In general, a continuous function f(x) has not just one antiderivative but an entire family of functions of the form F(x) + k, where k is a constant.
Family of Antiderivatives
The family of antiderivatives of a function f(x) consists of all functions of the form F(x) + k, where k is an arbitrary constant.
$$ F(x) + k $$
This holds because the derivative of a constant is always zero:
$$ D[F(x) + k] = D[f(x)] + D[k] = D[f(x)] + 0 $$
Example: The derivatives of F(x) = x2 + 3 and G(x) = x2 + 5 are both equal to 2x: $$ F'(x) = D[x^2 + 3] = 2x \\ G'(x) = D[x^2 + 5] = 2x $$ This is why the indefinite integral of 2x is written as: $$ \int 2x \: dx = x^2 + k $$ This notation captures all antiderivatives, including F(x), G(x), and the infinitely many others differing only by a constant.
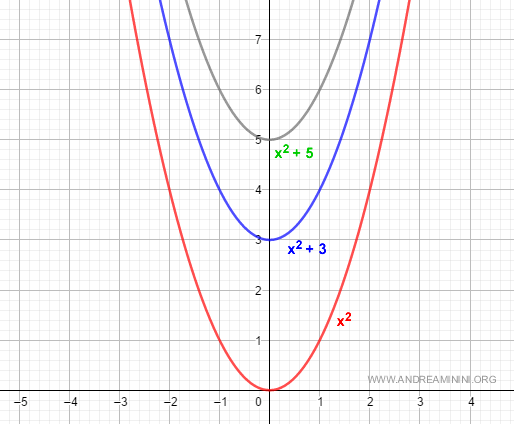
So, the indefinite integral of f(x) represents the entire family of antiderivatives, expressed as a specific antiderivative F(x) plus an arbitrary constant k:
$$ F(x) = \int_a^b f(x) \: dx $$ with $$ f(x) = F'(x) + k $$
Put differently:
If F(x) and G(x) are both antiderivatives of the same continuous function f(x) on [a, b], then there exists a constant k such that: $$ G(x) = F(x) + k \quad \text{for all } x \in [a, b] $$
Proof
Define a new function H(x) as the difference between G(x) and F(x):
$$ H(x) = G(x) - F(x) $$
Example: Let F(x) = x^2 + 3 and G(x) = x^2 + 5, both antiderivatives of f(x) = 2x. Then: $$ H(x) = G(x) - F(x) = (x^2 + 5) - (x^2 + 3) $$
The derivative of H(x) is zero:
$$ H'(x) = G'(x) - F'(x) $$
Since G'(x) = f(x) and F'(x) = f(x), their difference is zero:
$$ H'(x) = f(x) - f(x) = 0 $$
Example: $$ D[H(x)] = D[G(x)] - D[F(x)] = D[x^2 + 5] - D[x^2 + 3] = 2x - 2x = 0 $$
By Lagrange’s Mean Value Theorem, for any x in [a, b], there exists some point \( x_0 \in [a, x] \) such that:
$$ H(x) - H(a) = H'(x_0) \cdot (x - a) $$
Since H'(x) = 0 throughout the interval, we have:
$$ H(x) - H(a) = 0 \cdot (x - a) = 0 $$
Thus, H(x) = H(a), meaning H(x) is constant for all x in (a, b].
It follows that:
$$ H(x) = G(x) - F(x) \Rightarrow G(x) = F(x) + H(x) $$
Since H(x) is constant, we can write:
$$ G(x) = F(x) + k $$
Antiderivatives Are Continuous Functions
If \( F(x) \) is an antiderivative of a function \( f(x) \) that is continuous on an interval (a, b), then \( F(x) \) must also be continuous on that interval.
This is a direct consequence of the Fundamental Theorem of Calculus.
If a function f(x) is continuous, then there exists a function F(x) such that \( F'(x) = f(x) \).
Since f(x) arises as the derivative of F(x), it implies that F(x) must itself be continuous.
Example
Consider the function:
$$ f(x) = x^2 $$
This function is continuous on the open interval \((-1, 1)\).
An antiderivative of \( f(x) = x^2 \) is:
$$ F(x) = \frac{x^3}{3} + C $$
where \( C \) is an arbitrary constant.
Since f(x) is continuous on \((-1, 1)\), its antiderivative F(x) is also continuous on the same interval.
This example illustrates that the continuity of f(x) ensures the continuity of any antiderivative F(x).
Note: If \( f(x) \) is not continuous on (a, b), the situation changes significantly. There may be no antiderivative F(x) defined across the entire interval, or F(x) may still exist but behave differently. Here are two illustrative cases:
- Case 1: The function \( f(x) = \frac{1}{x} \) is discontinuous at \( x = 0 \), and its antiderivative \( F(x) = \ln |x| + C \) is also undefined at that point. In this case, the antiderivative reflects the discontinuity of f(x).
- Case 2: The function \( f(x) = \frac{1}{\sqrt{|x|}} \) is undefined at \( x = 0 \), yet its antiderivative \( F(x) = 2\sqrt{|x|} \) is continuous at that same point. This shows that an antiderivative can remain continuous even when the original function is not.
These examples highlight how the continuity of an antiderivative depends on the properties of the original function, but does not necessarily mirror its discontinuities.
And so on.
