Multiple (or Double) Integrals

What Are Multiple Integrals?

Multiple integrals - such as double and triple integrals - are definite integrals of functions involving two or more variables (i.e., dimensions). $$ \int f(x,y) \ dx \ dy $$ $$ \int f(x,y,z) \ dx \ dy \ dz $$

Integrals over two variables are referred to as double integrals, while those involving three variables are known as triple integrals.

What Are They Used For?

A double integral of a function of two variables calculates the volume under the surface defined by the function over a specific region in the plane.

Note: Just like single-variable definite integrals, multivariable integrals obey the same fundamental properties.

Double Integral

The multiple integral of a function \( f(x,y) \) of two variables (i.e., in two dimensions) is called a double integral.

It is typically denoted using a double integral sign:

$$ \int f(x,y) \ dx \ dy = \iint f(x,y) \ dx \ dy $$

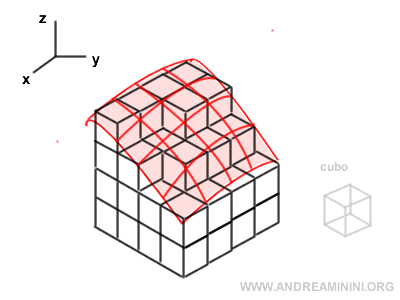
In a double integral, the region of integration is partitioned into small squares, and the function values over these elements are summed.

The value of the integral is obtained as the limit of this sum when the area of each square becomes infinitesimally small.

Triple Integral

The multiple integral of a function \( f(x,y,z) \) of three variables (i.e., in three dimensions) is known as a triple integral.

It is commonly expressed using a triple integral symbol:

$$ \int f(x,y,z) \ dx \ dy \ dz = \iiint f(x,y,z) \ dx \ dy \ dz $$

In the case of a triple integral, the domain of integration is divided into tiny cubes, and the function is evaluated and summed over each.

The integral corresponds to the limit of this sum as the volume of each cube approaches zero.

And so on.