Integration by Substitution

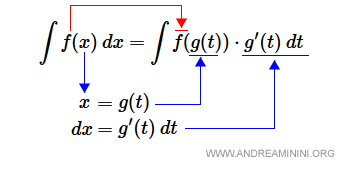
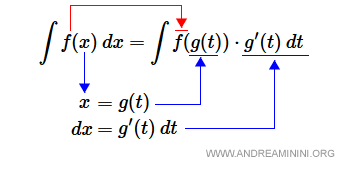
Let f(x) be a continuous function, and g(x) a differentiable function with continuous derivative. Then: $$ \int f(x) \: dx = \int f(g(t)) \cdot g'(t) \: dt $$ where \( x = g(t) \).

What is it for?

Integration by substitution is a standard method for evaluating indefinite integrals.

Two ways to apply substitution

This formula can be applied in either direction, depending on the structure of the integrand.

• First approach: Replace the variable \( x \) with the function \( g(t) \), and substitute \( dx \) with \( g'(t)\,dt \). The function f() stays the same, but the variable changes.
  
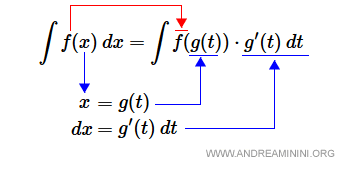
• Second approach: If the integrand is a composite function of the form \( f(g(x)) \cdot g'(x) \), you can simplify by substituting both \( g(x) \) and \( g'(x) \) with a new variable \( t \) and \( dt \).
  

Which method should you use? That depends on the integrand. In some cases, the first approach works better; in others, the second is more efficient. There’s no universal rule - the key is practice and familiarity with different types of functions.

Worked Examples

Example 1

Evaluate the integral:

$$ \int \frac{ \sin \sqrt{x} }{\sqrt{x}} \: dx $$

We'll apply the first substitution method.

The expression \( \sqrt{x} \) is the part that makes this integral challenging.

To simplify, we set \( t = \sqrt{x} \), then express x and dx in terms of t:

$$ t = \sqrt{x} $$

$$ x = t^2 $$

$$ dx = \frac{d}{dt}(t^2) \, dt = 2t \, dt $$

Substituting into the integral:

$$ \int \frac{ \sin \sqrt{x} }{\sqrt{x}} \: dx = \int \frac{ \sin t }{t} \cdot 2t \: dt $$

$$ = \int \sin t \cdot 2 \: dt $$

$$ = 2 \cdot \int \sin t \: dt $$

$$ = -2 \cos t + c $$

Back-substituting \( t = \sqrt{x} \):

$$ = -2 \cos(\sqrt{x}) + c $$

Example 2

Now consider:

$$ \int \cos x \cdot \sin ( \sin x ) \: dx $$

The integrand is the product of \( \cos x \) and a composite function \( \sin(\sin x) \).

Since \( \cos x \) is the derivative of the inner function \( \sin x \), this is a clear case for the second substitution method.

Let’s substitute:

$$ t = \sin x $$

Then:

$$ dt = \cos x \: dx $$

Substituting into the integral:

$$ \int \cos x \cdot \sin ( \sin x ) \: dx = \int \sin(t) \: dt $$

Which is a basic integral:

$$ = -\cos t + c $$

Returning to x:

$$ = -\cos(\sin x) + c $$

Example 3

Let’s evaluate:

$$ \int \frac{1}{\sqrt{x} - 3} \: dx $$

We’ll use the first substitution method again.

Let \( x = t^2 \), so:

$$ dx = 2t \: dt $$

Substitute into the integral:

$$ \int \frac{1}{\sqrt{x} - 3} \: dx = \int \frac{1}{t - 3} \cdot 2t \: dt $$

$$ = 2 \cdot \int \frac{t}{t - 3} \: dt $$

Now rewrite the numerator:

$$ = 2 \cdot \int \frac{(t - 3) + 3}{t - 3} \: dt $$

Split the integral using linearity:

$$ = 2 \cdot \left[ \int 1 \: dt + 3 \cdot \int \frac{1}{t - 3} \: dt \right] $$

Integrate term by term:

$$ = 2 \cdot \left[ t + 3 \log |t - 3| \right] + c $$

Now substitute back \( t = \sqrt{x} \):

$$ = 2 \sqrt{x} + 6 \log | \sqrt{x} - 3 | + c $$

So the solution is:

$$ \int \frac{1}{\sqrt{x} - 3} \: dx = 2 \sqrt{x} + 6 \log | \sqrt{x} - 3 | + c $$

Proof and Explanation

Integration by substitution is grounded in the chain rule for derivatives.

$$ \frac{d}{dt}F(g(t)) = F'(g(t)) \cdot g'(t) $$

Integrating both sides:

$$ \int \frac{d}{dt}F(g(t)) \: dt = \int F'(g(t)) \cdot g'(t) \: dt $$

Since integration and differentiation cancel each other:

$$ F(g(t)) = \int F'(g(t)) \cdot g'(t) \: dt $$

And if \( F'(g(t)) = f(g(t)) \), then:

$$ F(g(t)) = \int f(g(t)) \cdot g'(t) \: dt $$

So, by definition:

$$ \int f(g(t)) \: dt = \int f(g(t)) \cdot g'(t) \: dt $$

Now, using \( x = g(t) \), we rewrite the left-hand side as:

$$ \int f(x) \: dx = \int f(g(t)) \cdot g'(t) \: dt $$

And so on.